Determining features in the application of redundancy for the thermistor cubic transformation function using computer simulation

Authors

DOI:

https://doi.org/10.15587/1729-4061.2024.297619

Keywords:

redundant methods, instability of transformation function parameters, accuracy improvement, platinum thermistor

Abstract

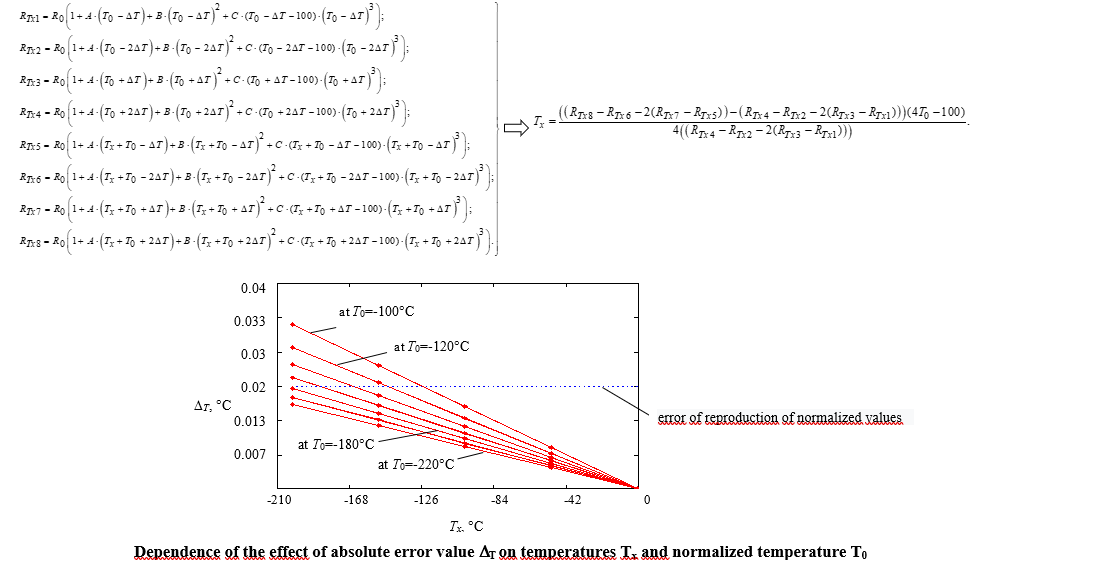
The object of research is the process of temperature measurement with a platinum thermistor. We have conducted studies on the cubic transformation function of the thermistor when using redundancy that yielded the equation of redundant measurements of the desired temperature. Owing to this, it became possible to directly apply the resulting equation without additional measures to linearize the function of the thermistor transformation. In addition, the obtained value of the desired temperature does not depend on the values of the parameters of the cubic transformation function and their deviations from the nominal values. Experimental studies have proven that the value of the normalized temperature T0 has a greater influence on the result of redundant measurements and the value of the normalized temperature DT on the entire range of measured temperatures Tx is almost unaffected. The best accuracy results (value of relative error δ=0.02 %) were obtained at T0 values lower than –60 °C. When the error of reproduction of normalized temperatures increased from ±0.02 °C to ±0.1 °C, the best accuracy results (value of relative error δ=0.06 %) were obtained at values of normalized temperature T0 below –130 °C. Analysis of results of the absolute error DT revealed that with an error of reproduction of normalized temperatures of ±0.02 °C and at T0=–180 °C, its value does not exceed 0.02 °C, that is, it is within the error of reproduction of normalized temperatures. This allows us to state that it is recommended to use sources of standardized temperatures of high accuracy during measurement control.

Thus, there are reasons to assert the prospect for redundant measurements when directly measuring temperature with a thermistor with a cubic transformation function with high accuracy

Author Biographies

Volodymyr Shcherban’, Kyiv National University of Technologies and Design

Doctor of Technical Sciences, Professor, Head of Department

Department of Computer Science

Hanna Korohod, Kyiv National University of Technologies and Design

PhD, Associate Professor

Department of Computer Science

Oksana Kolysko, Kyiv National University of Technologies and Design

PhD, Associate Professor

Department of Computer Science

Anton Kyrychenko, Kyiv National University of Technologies and Design

PhD, Associate Professor

Department of Computer Science

Yury Shcherban’, State Higher Educational Establishment "Kyiv College of Light Industry"

Doctor of Technical Sciences, Professor, Head of Department

Department of Light Industry Technologies

Ganna Shchutska, State Higher Educational Establishment "Kyiv College of Light Industry"

Doctor of Technical Sciences, Associate Professor

Director

Department of Light Industry Technologies

References

  1. Horbatyi, I. V. (2017). Improving measuring accuracy of inharmonious signal voltage under the additive noise condition. Tekhnolohiya i konstruiuvannia v elektronniy aparaturi, 1-2, 7–15. https://doi.org/10.15222/tkea2017.1-2.07
  2. Rishan, O. Y., Matvienko, N. V. (2014). Strukturni metody pidvyshchennia tochnosti vymiriuvan v avtomatychnykh systemakh dozuvannia sypkykh materialiv z vykorystanniam mahnitopruzhnykh pervynnykh vymiriuvalnykh peretvoriuvachiv zusyllia. Naukovo-tekhnichna informatsiya, 4, 47–51. Available at: http://nbuv.gov.ua/UJRN/NTI_2014_4_11
  3. Lappo, I., Chervotoka, О., Herashchenko, M., Prykhodko, S. (2022). Basic principles of improving the accuracy of temperature measurement by non-contact methods. Scientific works Of State Scientific Research Institute of Armament and Military Equipment Testing and Certification, 14 (4), 110–117. https://doi.org/10.37701/dndivsovt.14.2022.12
  4. Dorozinska, H. V. (2020). Evaluation Numerical Methods Effectiveness for Processing of Measurement Results by Improved SPR-Sensor. Visnyk of Vinnytsia Politechnical Institute, 149 (2), 7–13. https://doi.org/10.31649/1997-9266-2020-149-2-7-13
  5. Vdovichenko, A., Tuz, J. (2018). Accuracy enhancement of active power measurement with significant reactive load by creation of the shunt middle point. Measuring Equipment and Metrology, 79 (1), 76–81. https://doi.org/10.23939/istcmtm2018.01.076
  6. Pan, D., Jiang, Z., Gui, W., Yang, C., Xie, Y., Jiang, K. (2018). A method for improving the accuracy of infrared thermometry under the influence of dust. IFAC-PapersOnLine, 51 (21), 246–250. https://doi.org/10.1016/j.ifacol.2018.09.426
  7. Melnyk, V. G., Borschov, P. I., Beliaev, V. K., Vasylenko, O. D., Lameko, O. L., Slitskiy, O. V. (2020). Basic measuring module for implementation of the high-precision devices for determining the impedance parameters in a wide frequency range. Proceedings of the Institute of Electrodynamics of the National Academy of Sciences of Ukraine, 56, 20–23. https://doi.org/10.15407/publishing2020.56.020
  8. Boyko, O., Barylo, G., Holyaka, R., Hotra, Z., Ilkanych, K. (2018). Development of signal converter of thermal sensors based on combination of thermal and capacity research methods. Eastern-European Journal of Enterprise Technologies, 4 (9 (94)), 36–42. https://doi.org/10.15587/1729-4061.2018.139763
  9. Rishan, O. Y., Andriyuk, I. V. (2018). Linearization method of analog signals of primary measuring transducers with sinusoidal or cosine-wave conversion characteristics. Science, Technologies, Innovations, 2, 54–60. Available at: https://nti.ukrintei.ua/?page_id=1256
  10. Koritsoglou, K., Christou, V., Ntritsos, G., Tsoumanis, G., Tsipouras, M. G., Giannakeas, N., Tzallas, A. T. (2020). Improving the Accuracy of Low-Cost Sensor Measurements for Freezer Automation. Sensors, 20 (21), 6389. https://doi.org/10.3390/s20216389
  11. Lewis, G., Merken, P., Vandewal, M. (2018). Enhanced Accuracy of CMOS Smart Temperature Sensors by Nonlinear Curvature Correction. Sensors, 18 (12), 4087. https://doi.org/10.3390/s18124087
  12. Bedenik, G., Souza, M., Carvalho, E. A. N., Molina, L., Montalvao, J., Freire, R. (2022). Analysis of Parameters Influence in a MOX Gas Sensor Model. 2022 IEEE International Instrumentation and Measurement Technology Conference (I2MTC). https://doi.org/10.1109/i2mtc48687.2022.9806695
  13. Koestoer, R. A., Saleh, Y. A., Roihan, I., Harinaldi. (2019). A simple method for calibration of temperature sensor DS18B20 waterproof in oil bath based on Arduino data acquisition system. AIP Conference Proceedings. https://doi.org/10.1063/1.5086553
  14. Rajesh, R. J., Shtessel, Y., Edwards, C. (2020). Accuracy improvement of dynamic sensors using sliding mode observers with dynamic extension. Sensors and Actuators A: Physical, 316, 112396. https://doi.org/10.1016/j.sna.2020.112396
  15. Kvashuk, D. M., Lipkov, O. Ye. (2023). A new method of automatic correction of systematic errors of voltage converters. Visnyk of Kherson National Technical University, 2 (85), 29–36. https://doi.org/10.35546/kntu2078-4481.2023.2.3
  16. Belo, F. A., Soares, M. B., Lima Filho, A. C., Lima, T. L. de V., Adissi, M. O. (2023). Accuracy and Precision Improvement of Temperature Measurement Using Statistical Analysis/Central Limit Theorem. Sensors, 23 (6), 3210. https://doi.org/10.3390/s23063210
  17. Kondratov, V. T. (2014). The problems solved by methods of redundant measurements. Vymiriuvalna ta obchysliuvalna tekhnika v tekhnolohichnykh protsesakh – 2014 (VOTTP-14 2014). Odesa, 26–30. Available at: https://docplayer.net/49537211-Materiali-xiii-mizhnarodnoyi-naukovo-tehnichnoyi-konferenciyi.html
  18. Shcherban, V., Korogod, G., Chaban, V., Kolysko, O., Shcherban’, Y., Shchutska, G. (2019). Computer simulation methods of redundant measurements with the nonlinear transformation function. Eastern-European Journal of Enterprise Technologies, 2 (5 (98)), 16–22. https://doi.org/10.15587/1729-4061.2019.160830
  19. Shcherban’, V., Korogod, G., Kolysko, O., Kolysko, M., Shcherban’, Y., Shchutska, G. (2020). Computer simulation of multiple measurements of logarithmic transformation function by two approaches. Eastern-European Journal of Enterprise Technologies, 6 (4 (108)), 6–13. https://doi.org/10.15587/1729-4061.2020.218517
  20. Shcherban’, V., Korogod, G., Kolysko, O., Kolysko, M., Shcherban’, Y., Shchutska, G. (2021). Computer simulation of logarithmic transformation function to expand the range of high-precision measurements. Eastern-European Journal of Enterprise Technologies, 2 (9 (110)), 27–36. https://doi.org/10.15587/1729-4061.2021.227984
  21. Shcherban’, V., Korogod, G., Kolysko, O., Volivach, A., Shcherban’, Y., Shchutska, G. (2022). Computer modeling in the study of the effect of normalized quantities on the measurement accuracy of the quadratic transformation function. Eastern-European Journal of Enterprise Technologies, 2 (5 (116)), 6–16. https://doi.org/10.15587/1729-4061.2022.254337
  22. Lebedev, V., Laukhina, E., Laukhin, V., Somov, A., Baranov, A. M., Rovira, C., Veciana, J. (2017). Investigation of sensing capabilities of organic bi-layer thermistor in wearable e-textile and wireless sensing devices. Organic Electronics, 42, 146–152. https://doi.org/10.1016/j.orgel.2016.12.034
Determining features in the application of redundancy for the thermistor cubic transformation function using computer simulation

Downloads

Published

2024-02-28

How to Cite

Shcherban’, V., Korohod, H., Kolysko, O., Kyrychenko, A., Shcherban’, Y., & Shchutska, G. (2024). Determining features in the application of redundancy for the thermistor cubic transformation function using computer simulation. Eastern-European Journal of Enterprise Technologies, 1(5 (127), 33–40. https://doi.org/10.15587/1729-4061.2024.297619

Issue

Vol. 1 No. 5 (127) (2024): Applied physics

Section

Applied physics

License

Copyright (c) 2024 Volodymyr Shcherban’, Hanna Korohod, Oksana Kolysko, Anton Kyrychenko, Yury Shcherban’, Ganna Shchutska

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.