Assessment of QOS indicators of a network with UDP and TCP traffic under a node peak load mode
DOI:
https://doi.org/10.15587/1729-4061.2024.299124Keywords:
Markov model, network traffic, network node, mass service systemAbstract
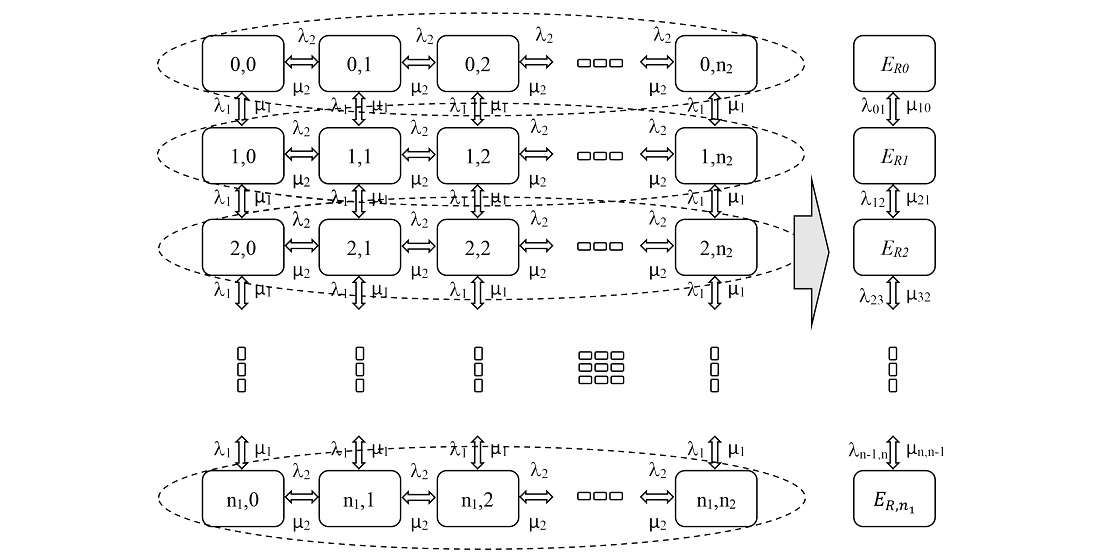
The object of research is Markov models of network nodes with UDP (User Datagram Protocol) and TCP (Transmission Control Protocol) traffic and their differences.
The task solved is the lack of Markov models of network nodes describing the behavior of TCP traffic from the point of view of packet retransmissions and packet delivery guarantees.
Markov models of network nodes describing traffic behavior with guaranteed packet delivery have been further advanced. Given the comparison of the models, the differences from the classic models serving TCP traffic were shown, for each packet flow, an additional dimensionally was added to the graph of states and transitions, which takes into account the retransmission of a lost packet. The comparison graph shows similar behavior of queue length and packet loss for both types of traffic. But the nature of the curves is different. With TCP traffic, packet loss can exceed 5 percent. In addition, lost packets must be retransmitted, which increases the load on the network node.
More failures and packet queue lengths at a network node during peak load typically occur with TCP traffic compared to UDP traffic. At peak load, the difference in service failures can reach 20–30 percent. The main reason is that TCP uses flow control and rate-limiting mechanisms to avoid network congestion and ensure efficient data transfer between nodes.
The Markov model of TCP traffic requires an additional dimensionally on the graph of states and transitions, which affects the behavior of queues and packet failures.
The investigated problem was solved due to the universality and diversity of the mathematical apparatus of Markov mass service systems.
The results could be used in network modeling software products for building and reengineering the topology of electronic communications networks at enterprises and organizations
References
- Kleinrock, L. (1975). Queueing Systems. Vol. I. Theory. Wiley, 417.
- Estes, A. S., Ball, M. O. (2020). Facets of the Stochastic Network Flow Problem. SIAM Journal on Optimization, 30 (3), 2355–2378. https://doi.org/10.1137/19m1286049
- Moormann, L., Schouten, R. H. J., van de Mortel-Fronczak, J. M., Fokkink, W. J., Rooda, J. E. (2023). Synthesis and Implementation of Distributed Supervisory Controllers With Communication Delays. IEEE Transactions on Automation Science and Engineering, 20 (3), 1591–1606. https://doi.org/10.1109/tase.2023.3260442
- Singla, N., Kalra, S. (2021). Performance Analysis of a Two-Dimensional State Multiserver Markovian Queueing Model with Reneging Customers. Recent Trends in Mathematical Modeling and High Performance Computing, 313–330. https://doi.org/10.1007/978-3-030-68281-1_24
- Chakravarthy, S. R., Rumyantsev, A. (2020). Analytical and simulation studies of queueing-inventory models with MAP demands in batches and positive phase type services. Simulation Modelling Practice and Theory, 103, 102092. https://doi.org/10.1016/j.simpat.2020.102092
- Aouad, A., Saritaç, Ö. (2020). Dynamic Stochastic Matching Under Limited Time. Proceedings of the 21st ACM Conference on Economics and Computation. https://doi.org/10.1145/3391403.3399524
- Harchol-Balter, M. (2021). Open problems in queueing theory inspired by datacenter computing. Queueing Systems, 97 (1-2), 3–37. https://doi.org/10.1007/s11134-020-09684-6
- Casas, J. M., Ladra, M., Rozikov, U. A. (2019). Markov processes of cubic stochastic matrices: Quadratic stochastic processes. Linear Algebra and Its Applications, 575, 273–298. https://doi.org/10.1016/j.laa.2019.04.016
- Cruz, F. R. B., Almeida, M. A. C., D’Angelo, M. F. S. V., van Woensel, T. (2018). Traffic Intensity Estimation in Finite Markovian Queueing Systems. Mathematical Problems in Engineering, 2018, 1–15. https://doi.org/10.1155/2018/3018758
- Maia, C.-A. (2022). Stochastic Timed Discrete-Event Systems: Modular Modeling and Performance Evaluation Through Markovian Jumps. IEEE Access, 10, 108332–108341. https://doi.org/10.1109/access.2022.3213697
- Barabash, O., Kolumbet, V. (2023). Research of mass service systems on the base of simulation modeling taking into account the multi-agent approach. Infocommunication and computer technologies, 2 (04), 115–121. https://doi.org/10.36994/2788-5518-2022-02-04-12
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2024 Pavlo Pustovoitov, Vitalii Voronets, Oleksandr Voronets, Halyna Sokol, Maksym Okhrymenko

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.









