Оцінка показників QOS мережі з UDP та TCP трафіком у режимі пікового навантаження вузла
DOI:
https://doi.org/10.15587/1729-4061.2024.299124Ключові слова:
марківська модель, мережевий трафік, вузол мережі, система масового обслуговуванняАнотація
Об’єктом дослідження є марківські моделі вузлів мереж з UDP (User Datagram Protocol, протокол користувацьких дейтаграм) та TCP (Transmission Control Protocol, протокол керування передачею) трафіком та їх відмінності.
Проблема, що вирішувалася, – відсутність марківських моделей вузлів мереж, що описують поведінку TCP трафіку з точки зору повторних передач пакетів та гарантування доставки пакетів.
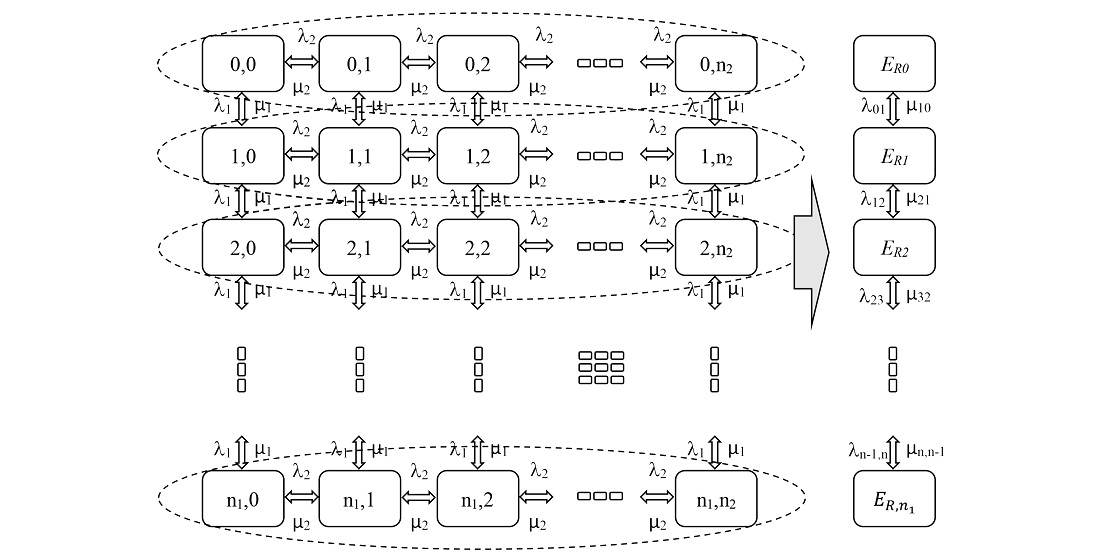
Отримали подальший розвиток марківські моделі вузлів мереж, що описують поведінку трафіку з гарантованою доставкою пакетів. За рахунок порівняння моделей показані відмінності від класичних моделей, що обслуговують TCP трафік, для кожного потоку пакетів додано додаткову розмірність на графу станів та переходів, яка враховує повторну передачу втраченого пакету. Порівняльний графік показує схожу поведінку довжини черг та втрат пакетів для обох видів трафіку. Але характер кривих відрізняється. При TCP трафіку втрат пакетів може бути більше на 5 відсотків. Крім цього, втрачені пакети треба передавати повторно, це підвищує навантаження на вузол мережі.
Більше відмов та довжини черги пакетів на вузлі мережі при піковому навантаженні зазвичай відбувається при TCP трафіку порівняно з UDP трафіком. При піковому навантажені відмінність у відмовах в обслуговуванні може досягати 20–30 відсотків. Основна причина полягає в тому, що TCP використовує механізми керування потоком і визначення швидкості передачі даних, щоб уникнути перевантаження мережі та гарантувати ефективну передачу даних між вузлами.
Марківська модель TCP трафіку потребує додаткову розмірність на графі станів та переходів, що впливає на поведніку черг, відмов пакетів.
Досліджувана проблема вирішена за рахунок універсальності та різноманітності математичного апарату марківських систем масового обслуговування.
Отримані результати можуть бути використані у програмних продуктах моделювання мереж для побудови та реінжениринга топології мереж електронних комунікацій підприємст та організацій
Посилання
- Kleinrock, L. (1975). Queueing Systems. Vol. I. Theory. Wiley, 417.
- Estes, A. S., Ball, M. O. (2020). Facets of the Stochastic Network Flow Problem. SIAM Journal on Optimization, 30 (3), 2355–2378. https://doi.org/10.1137/19m1286049
- Moormann, L., Schouten, R. H. J., van de Mortel-Fronczak, J. M., Fokkink, W. J., Rooda, J. E. (2023). Synthesis and Implementation of Distributed Supervisory Controllers With Communication Delays. IEEE Transactions on Automation Science and Engineering, 20 (3), 1591–1606. https://doi.org/10.1109/tase.2023.3260442
- Singla, N., Kalra, S. (2021). Performance Analysis of a Two-Dimensional State Multiserver Markovian Queueing Model with Reneging Customers. Recent Trends in Mathematical Modeling and High Performance Computing, 313–330. https://doi.org/10.1007/978-3-030-68281-1_24
- Chakravarthy, S. R., Rumyantsev, A. (2020). Analytical and simulation studies of queueing-inventory models with MAP demands in batches and positive phase type services. Simulation Modelling Practice and Theory, 103, 102092. https://doi.org/10.1016/j.simpat.2020.102092
- Aouad, A., Saritaç, Ö. (2020). Dynamic Stochastic Matching Under Limited Time. Proceedings of the 21st ACM Conference on Economics and Computation. https://doi.org/10.1145/3391403.3399524
- Harchol-Balter, M. (2021). Open problems in queueing theory inspired by datacenter computing. Queueing Systems, 97 (1-2), 3–37. https://doi.org/10.1007/s11134-020-09684-6
- Casas, J. M., Ladra, M., Rozikov, U. A. (2019). Markov processes of cubic stochastic matrices: Quadratic stochastic processes. Linear Algebra and Its Applications, 575, 273–298. https://doi.org/10.1016/j.laa.2019.04.016
- Cruz, F. R. B., Almeida, M. A. C., D’Angelo, M. F. S. V., van Woensel, T. (2018). Traffic Intensity Estimation in Finite Markovian Queueing Systems. Mathematical Problems in Engineering, 2018, 1–15. https://doi.org/10.1155/2018/3018758
- Maia, C.-A. (2022). Stochastic Timed Discrete-Event Systems: Modular Modeling and Performance Evaluation Through Markovian Jumps. IEEE Access, 10, 108332–108341. https://doi.org/10.1109/access.2022.3213697
- Barabash, O., Kolumbet, V. (2023). Research of mass service systems on the base of simulation modeling taking into account the multi-agent approach. Infocommunication and computer technologies, 2 (04), 115–121. https://doi.org/10.36994/2788-5518-2022-02-04-12
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2024 Pavlo Pustovoitov, Vitalii Voronets, Oleksandr Voronets, Halyna Sokol, Maksym Okhrymenko

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.
Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.









