Development of a neural network with a layer of trainable activation functions for the second stage of the ensemble classifier with stacking
DOI:
https://doi.org/10.15587/1729-4061.2024.311778Keywords:
multilayer perceptron, neural network, ensemble classifier, weighting coefficients, classification of objects in imagesAbstract
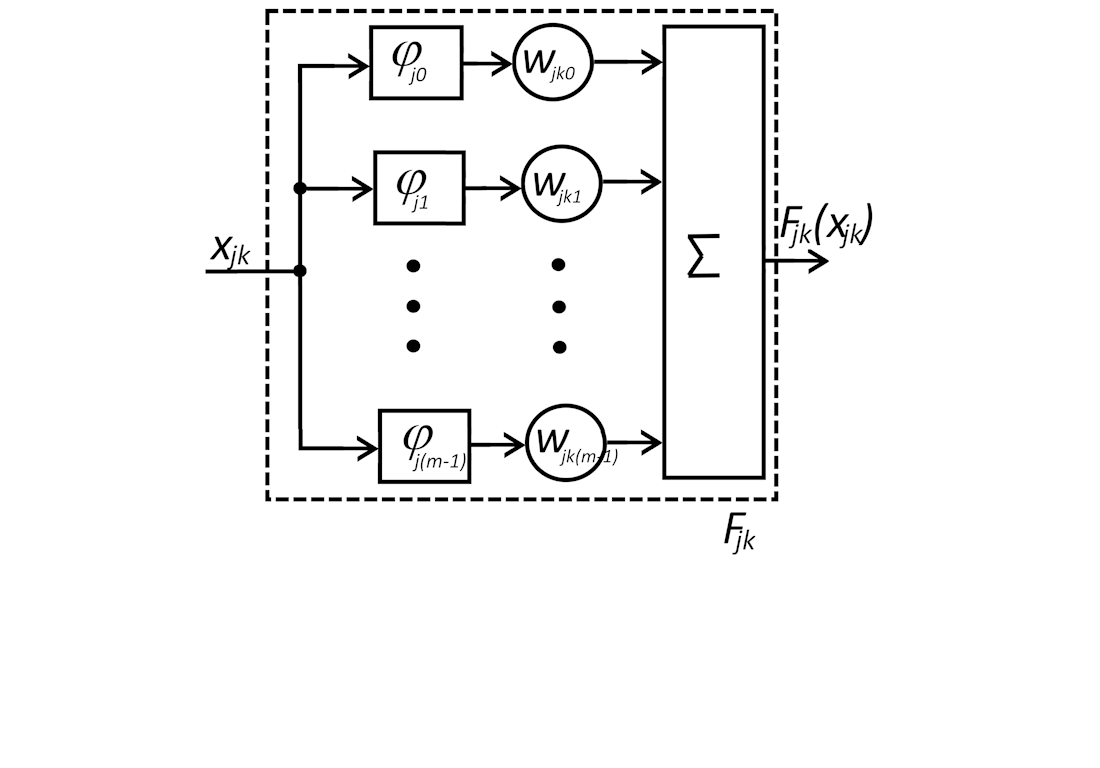
One of the promising directions for improving the quality of object recognition in images and parallelizing calculations is the use of ensemble classifiers with stacking. A neural network at the second level makes it possible to achieve the resulting quality of classification, which is significantly higher than each of the networks of the first level separately. The classification quality of the entire ensemble classifier with stacking depends on the efficiency of the neural networks at the first stage, their number, and the quality of the classification of the neural network of the second stage. This paper proposes a neural network architecture for the second stage of the ensemble classifier, which combines the approximating properties of traditional neurons and learning activation functions. Gaussian Radial Basis Functions (RBFs) were chosen to implement the learned activation functions, which are summed with the learned weights. The experimental studies showed that when working with the CIFAR-10 data set, the best results are obtained when six RBFs are used. A comparison with the use of multilayer perceptron (MLP) in the second stage showed a reduction in classification errors by 0.45–1.9 % depending on the number of neural networks in the first stage. At the same time, the proposed neural network architecture for the second degree had 1.69–3.7 times less learning coefficients than MLP. This result is explained by the fact that the use of an output layer with ordinary neurons allowed us not to enter into the architecture many learning activation functions for each output signal of the first stage, but to limit ourselves to only one. Since the results were obtained on the CIFAR-10 universal data set, a similar effect could be obtained on a large number of similar practical data sets.
References
- Rokach, L. (2019). Ensemble Learning. Series in Machine Perception and Artificial Intelligence. https://doi.org/10.1142/11325
- Galchonkov, O., Babych, M., Zasidko, A., Poberezhnyi, S. (2022). Using a neural network in the second stage of the ensemble classifier to improve the quality of classification of objects in images. Eastern-European Journal of Enterprise Technologies, 3 (9 (117)), 15–21. https://doi.org/10.15587/1729-4061.2022.258187
- Liu, Z., Wang, Y., Vaidya, S., Ruehle, F., Halverson, J., Soljačić, M. et al. (2024). KAN: Kolmogorov-Arnold Networks. arXiv. https://doi.org/10.48550/arXiv.2404.19756
- Hornik, K., Stinchcombe, M., White, H. (1989). Multilayer feedforward networks are universal approximators. Neural Networks, 2 (5), 359–366. https://doi.org/10.1016/0893-6080(89)90020-8
- Braun, J., Griebel, M. (2009). On a Constructive Proof of Kolmogorov’s Superposition Theorem. Constructive Approximation, 30 (3), 653–675. https://doi.org/10.1007/s00365-009-9054-2
- Hao, H., Zhang, X., Li, B., Zhou, A. (2024). A First Look at Kolmogorov-Arnold Networks in Surrogate-assisted Evolutionary Algorithms. arXiv. https://doi.org/10.48550/arXiv.2405.16494
- Drokin, I. (2024). Kolmogorov-Arnold Convolutions: Design Principles and Empirical Studies. arXiv. https://doi.org/10.48550/arXiv.2407.01092
- Tolstikhin, I., Houlsby, N., Kolesnikov, A., Beyer, L., Zhai, X., Unterthiner, T. et al. (2021). MLP-Mixer: An all-MLP Architecture for Vision. arXiv. https://doi.org/10.48550/arXiv.2105.01601
- Cheon, M. (2024). Demonstrating the efficacy of Kolmogorov-Arnold Networks in vision tasks. arXiv. https://doi.org/10.48550/arXiv.2406.14916
- Zhang, F., Zhang, X. (2024). GraphKAN: Enhancing Feature Extraction with Graph Kolmogorov Arnold Networks. arXiv. https://doi.org/10.48550/arXiv.2406.13597
- Xu, J., Chen, Z., Li, J., Yang, S., Wang, W., Hu, X. et al. (2024). FourierKAN-GCF: Fourier Kolmogorov-Arnold Network – An Effective and Efficient Feature Transformation for Graph Collaborative Filtering. arXiv. https://doi.org/10.48550/arXiv.2406.01034
- Vaca-Rubio, C. J., Blanco, L., Pereira, R., Caus, M. (2024). Kolmogorov-Arnold Networks (KANs) for Time Series Analysis. arXiv. https://doi.org/10.48550/arXiv.2405.08790
- Inzirillo, H., Genet, R. (2024). SigKAN: Signature-Weighted Kolmogorov-Arnold Networks for Time Series. arXiv. https://doi.org/10.48550/arXiv.2406.17890
- Ismayilova, A., Ismayilov, M. (2023). On the universal approximation property of radial basis function neural networks. Annals of Mathematics and Artificial Intelligence, 92 (3), 691–701. https://doi.org/10.1007/s10472-023-09901-x
- Li, Z. (2024). Kolmogorov-Arnold Networks are Radial Basis Function Networks. arXiv. https://doi.org/10.48550/arXiv.2405.06721
- Bao, X., Liu, G., Yang, G., Wang, S. (2020). Multi-instance Multi-label Text Categorization Algorithm Based on Multi-quadric Function Radial Basis Network Model. 2020 3rd International Conference on Artificial Intelligence and Big Data (ICAIBD), 1998, 133–136. https://doi.org/10.1109/icaibd49809.2020.9137478
- Basha Kattubadi, I., Murthy Garimella, R. (2020). Novel Deep Learning Architectures: Feature Extractor and Radial Basis Function Neural Network. 2020 International Conference on Computational Performance Evaluation (ComPE), 024–027. https://doi.org/10.1109/compe49325.2020.9200146
- He, Z.-R., Lin, Y.-T., Lee, S.-J., Wu, C.-H. (2018). A RBF Network Approach for Function Approximation. 2018 IEEE International Conference on Information and Automation (ICIA), 9, 105–109. https://doi.org/10.1109/icinfa.2018.8812435
- Panda, S., Panda, G. (2022). On the Development and Performance Evaluation of Improved Radial Basis Function Neural Networks. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 52 (6), 3873–3884. https://doi.org/10.1109/tsmc.2021.3076747
- Wu, C., Kong, X., Yang, Z. (2018). An Online Self-Adaption Learning Algorithm for Hyper Basis Function Neural Network. 2018 2nd IEEE Advanced Information Management,Communicates,Electronic and Automation Control Conference (IMCEC), 9, 215–220. https://doi.org/10.1109/imcec.2018.8469684
- Seydi, S. T. (2024). Exploring the Potential of Polynomial Basis Functions in Kolmogorov-Arnold Networks: A Comparative Study of Different Groups of Polynomials. arXiv. https://doi.org/10.48550/arXiv.2406.02583
- Seydi, S. T. (2024). Unveiling the Power of Wavelets: A Wavelet-based Kolmogorov-Arnold Network for Hyperspectral Image Classification. arXiv. https://doi.org/10.48550/arXiv.2406.07869
- Qiu, Q., Zhu, T., Gong, H., Chen, L., Ning, H. (2024). ReLU-KAN: New Kolmogorov-Arnold Networks that Only Need Matrix Addition, Dot Multiplication, and ReLU. arXiv. https://doi.org/10.48550/arXiv.2406.02075
- Krizhevsky, A. The CIFAR-10 dataset. Available at: https://www.cs.toronto.edu/~kriz/cifar.html
- Hassani, A., Walton, S., Shah, N., Abuduweili, A., Li, J., Shi, H. (2021). Escaping the Big Data Paradigm with Compact Transformers. arXiv. https://doi.org/10.48550/arXiv.2104.05704
- Guo, M.-H., Liu, Z.-N., Mu, T.-J., Hu, S.-M. (2022). Beyond Self-Attention: External Attention Using Two Linear Layers for Visual Tasks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1–13. https://doi.org/10.1109/tpami.2022.3211006
- Lee-Thorp, J., Ainslie, J., Eckstein, I., Ontanon, S. (2022). FNet: Mixing Tokens with Fourier Transforms. Proceedings of the 2022 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies. https://doi.org/10.18653/v1/2022.naacl-main.319
- Liu, H., Dai, Z., So, D. R., Le, Q. V. (2021). Pay Attention to MLPs. arXiv. https://doi.org/10.48550/arXiv.2105.08050
- Liu, Z., Lin, Y., Cao, Y., Hu, H., Wei, Y., Zhang, Z. et al. (2021). Swin Transformer: Hierarchical Vision Transformer using Shifted Windows. 2021 IEEE/CVF International Conference on Computer Vision (ICCV). https://doi.org/10.1109/iccv48922.2021.00986
- Brownlee, J. (2021). Weight Initialization for Deep Learning Neural Networks. Available at: https://machinelearningmastery.com/weight-initialization-for-deep-learning-neural-networks/
- Code examples. Computer vision. Keras. Available at: https://keras.io/examples/vision/
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2024 Oleg Galchonkov, Oleksii Baranov, Svetlana Antoshchuk, Oleh Maslov, Mykola Babych

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.









