Development of a mathematical model for managing schedule delays in air traffic operations
DOI:
https://doi.org/10.15587/1729-4061.2024.312342Keywords:
air traffic management, mathematical models, schedule delay management, optimization, operational efficiency, aviation industryAbstract
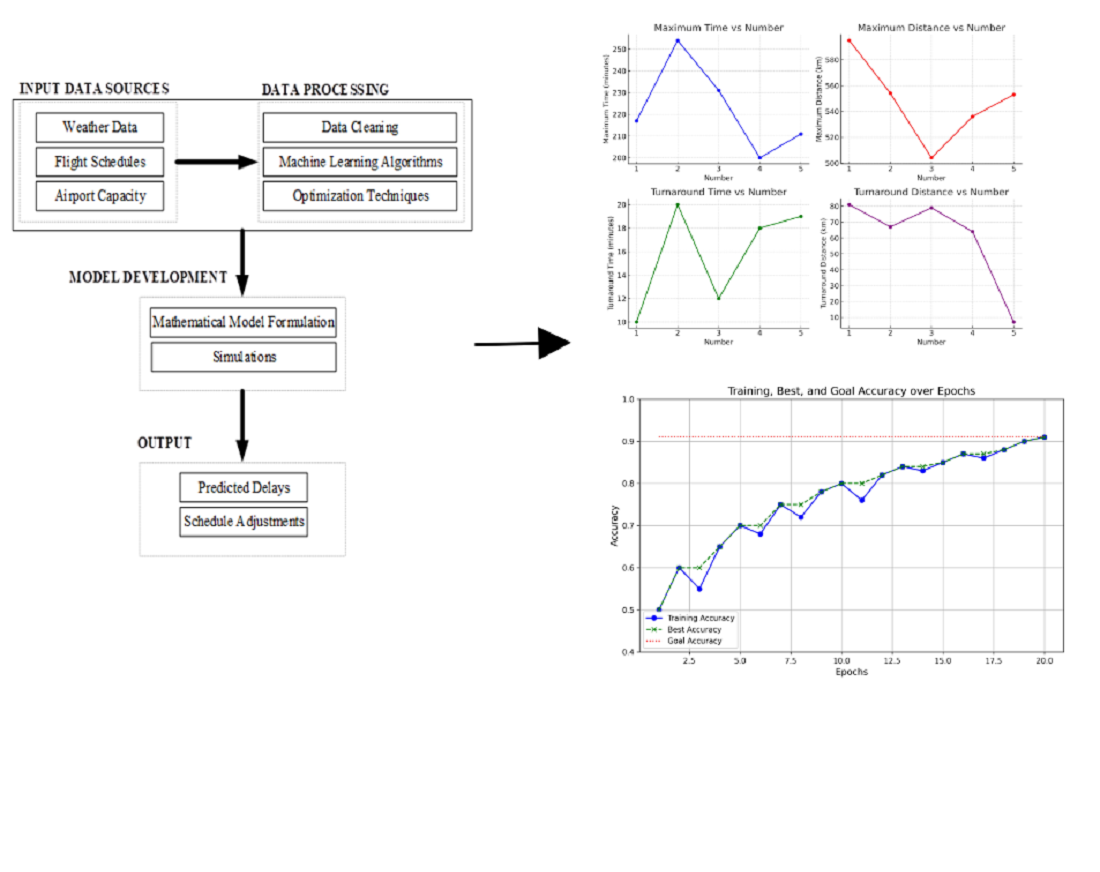
The object of this research is delay in air traffic operations. The problem in this research that must be solved is how to reduce the impact of frequent delays which cause time efficiency but cause increased operational costs and make customers dissatisfied with air traffic services and then there is time complexity which is difficult to overcome. The interpretation of this research is to analyze existing problems and then apply mathematical methods so that it is possible to develop a model that is able to dynamically optimize flight rescheduling which can be beneficial for customers in reducing waiting times. This model will consider many important variables in managing delay schedules including real-time weather conditions, aircraft availability, airport capacity so that the results of this model show the ability to reduce the frequency and duration of delays which can increase customer satisfaction. This application shows that the model developed has main characteristics such as flexibility in adjusting schedules in terms of delays and accuracy in predicting potential delays so that the problems analyzed and researched can be resolved effectively and efficiently. This model can predict schedule delays with an accuracy level of 90 % according to predetermined input variables. Then there are quantitative benefits in the form of reducing operational costs for delays, increasing prediction accuracy and optimizing flight schedules. Qualitatively there are benefits in customer satisfaction and faster and more effective decision making. The scope of this research includes managing flight schedules at airports and international hubs. Implementation of this model is important to ensure high operational efficiency and minimize the impact of delays in various operational conditions
References
- Kia, R., Shahnazari-Shahrezaei, P., Zabihi, S. (2016). Solving a multi-objective mathematical model for a Multi-Skilled Project Scheduling Problem by CPLEX solver. 2016 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), 1220–1224. https://doi.org/10.1109/ieem.2016.7798072
- Norouzi, G., Heydari, M., Noori, S., Bagherpour, M. (2015). Developing a Mathematical Model for Scheduling and Determining Success Probability of Research Projects Considering Complex-Fuzzy Networks. Journal of Applied Mathematics, 2015, 1–15. https://doi.org/10.1155/2015/809216
- Deng, R., Yang, Z., Chow, M.-Y., Chen, J. (2015). A Survey on Demand Response in Smart Grids: Mathematical Models and Approaches. IEEE Transactions on Industrial Informatics, 11 (3), 570–582. https://doi.org/10.1109/tii.2015.2414719
- Ball, M. O., Chen, C.-Y., Hoffman, R., Vossen, T. (2001). Collaborative Decision Making in Air Traffic Management: Current and Future Research Directions. New Concepts and Methods in Air Traffic Management, 17–30. https://doi.org/10.1007/978-3-662-04632-6_2 2
- Samà, M., D’Ariano, A., D’Ariano, P., Pacciarelli, D. (2017). Scheduling models for optimal aircraft traffic control at busy airports: Tardiness, priorities, equity and violations considerations. Omega, 67, 81–98. https://doi.org/10.1016/j.omega.2016.04.003
- Sandamali, G. G. N., Su, R., Sudheera, K. L. K., Zhang, Y. (2022). A Safety-Aware Real-Time Air Traffic Flow Management Model Under Demand and Capacity Uncertainties. IEEE Transactions on Intelligent Transportation Systems, 23 (7), 8615–8628. https://doi.org/10.1109/tits.2021.3083964
- Samà, M., D’Ariano, A., D’Ariano, P., Pacciarelli, D. (2015). Air traffic optimization models for aircraft delay and travel time minimization in terminal control areas. Public Transport, 7 (3), 321–337. https://doi.org/10.1007/s12469-015-0103-x
- Zhang, Y., Su, R., Li, Q., Cassandras, C. G., Xie, L. (2017). Distributed Flight Routing and Scheduling for Air Traffic Flow Management. IEEE Transactions on Intelligent Transportation Systems, 18 (10), 2681–2692. https://doi.org/10.1109/tits.2017.2657550
- Sridhar, B., Grabbe, S. R., Mukherjee, A. (2008). Modeling and Optimization in Traffic Flow Management. Proceedings of the IEEE, 96 (12), 2060–2080. https://doi.org/10.1109/jproc.2008.2006141
- Cai, K.-Q., Zhang, J., Xiao, M.-M., Tang, K., Du, W.-B. (2017). Simultaneous Optimization of Airspace Congestion and Flight Delay in Air Traffic Network Flow Management. IEEE Transactions on Intelligent Transportation Systems, 18 (11), 3072–3082. https://doi.org/10.1109/tits.2017.2673247
- Reitmann, S., Schultz, M. (2022). An Adaptive Framework for Optimization and Prediction of Air Traffic Management (Sub-)Systems with Machine Learning. Aerospace, 9 (2), 77. https://doi.org/10.3390/aerospace9020077
- Štimac, I., Vidović, A., Mihetec, T., Drljača, M. (2020). Optimization of Airport Capacity Efficiency by Selecting Optimal Aircraft and Airline Business Model. Sustainability, 12 (10), 3988. https://doi.org/10.3390/su12103988
- Rodríguez-Sanz, Á., Gómez Comendador, F., Arnaldo Valdés, R., Cordero García, J. M., Bagamanova, M. (2018). Uncertainty Management at the Airport Transit View. Aerospace, 5 (2), 59. https://doi.org/10.3390/aerospace5020059
- Dönmez, K., Aydoğan, E., Çetek, C., Maraş, E. E. (2022). The Impact of Taxiway System Development Stages on Runway Capacity and Delay under Demand Volatility. Aerospace, 10 (1), 6. https://doi.org/10.3390/aerospace10010006
- Higasa, K., Itoh, E. (2022). Controlling Aircraft Inter-Arrival Time to Reduce Arrival Traffic Delay via a Queue-Based Integer Programming Approach. Aerospace, 9 (11), 663. https://doi.org/10.3390/aerospace9110663
- Ivanov, N., Netjasov, F., Jovanović, R., Starita, S., Strauss, A. (2017). Air Traffic Flow Management slot allocation to minimize propagated delay and improve airport slot adherence. Transportation Research Part A: Policy and Practice, 95, 183–197. https://doi.org/10.1016/j.tra.2016.11.010
- Zámková, M., Rojík, S., Prokop, M., Stolín, R. (2022). Factors Affecting the International Flight Delays and Their Impact on Airline Operation and Management and Passenger Compensations Fees in Air Transport Industry: Case Study of a Selected Airlines in Europe. Sustainability, 14 (22), 14763. https://doi.org/10.3390/su142214763
- Zhi Jun, L., Alam, S., Dhief, I., Schultz, M. (2022). Towards a greener Extended-Arrival Manager in air traffic control: A heuristic approach for dynamic speed control using machine-learned delay prediction model. Journal of Air Transport Management, 103, 102250. https://doi.org/10.1016/j.jairtraman.2022.102250
- Pinto Neto, E. C., Baum, D. M., Almeida, J. R. de, Camargo, J. B., Cugnasca, P. S. (2023). Deep Learning in Air Traffic Management (ATM): A Survey on Applications, Opportunities, and Open Challenges. Aerospace, 10 (4), 358. https://doi.org/10.3390/aerospace10040358
- Jiménez-Martín, A., Tello, F., Mateos, A. (2020). A Variation of the ATC Work Shift Scheduling Problem to Deal with Incidents at Airport Control Centers. Mathematics, 8 (3), 321. https://doi.org/10.3390/math8030321
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2024 Sunardi Sunardi, Syahrul Humaidi, Marhaposan Situmorang, Marzuki Sinambela

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.









