Identifying a mechanism for the gripping ability of rolls and rolling at a stability limit under asymmetric loading

Authors

DOI:

https://doi.org/10.15587/1729-4061.2025.340835

Keywords:

loading asymmetry, counter-directed metal flow, loss of stability, stressed-strained state

Abstract

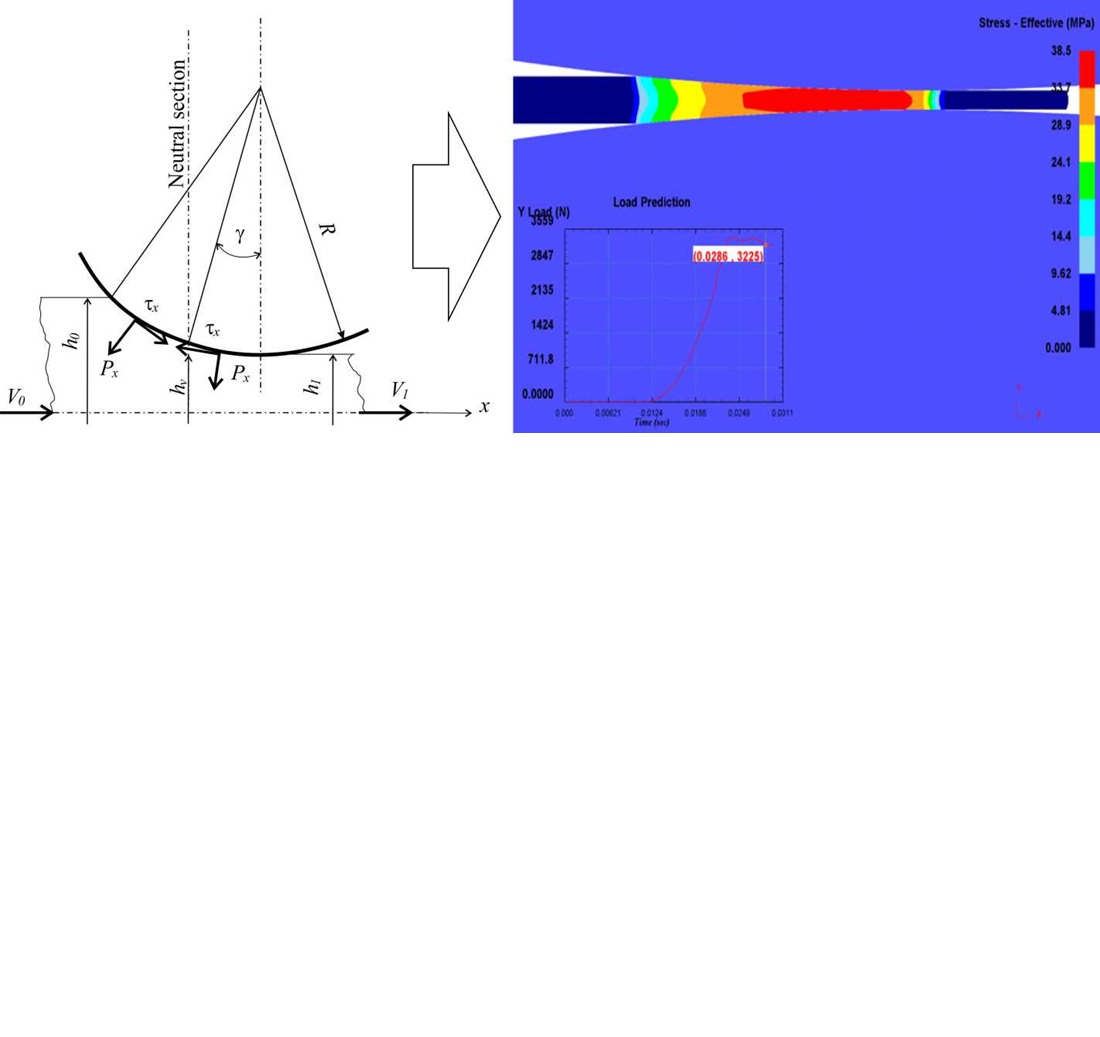
This study’s object is the stressed state of the plastic deformation site under conditions of load asymmetry when metal is gripped by rolls, under the determining modes of process stability. The task addressed is the implementation of shape change at the rolling process stability threshold related to a decreased force load under the increased strain impact.

A physical and mathematical model of a flat rolling theory problem has been built under conditions of multi-parameter factors affecting the gripping capacity of rolls and the stability of rolling process.

The plasticity theory problem was solved analytically using the method of argument of a function of a complex variable. The solution to the plane problem is shown, using the asymmetry of the process, the counter-directed flow of metal. The nonlinearity of the plasticity theory problem was taken into account.

Based on the mathematical model, a new force factor was identified and investigated: the force stretching factor from the lagging zone. A new single-zone deformation mode with minimum process stability was identified. The process was investigated under conditions of multiparameter influence on rolls gripping ability and its stability. The zones of reachability were established for a deformation focus shape factor within the range of 5.00...15.00. The mode of partial suppression of the zeroing factors of the metal stressed state was investigated under conditions of multi-parameter influence on the gripping ability of the rolls and the stability of the process. Stability indicators of transient modes were determined: at α = 0.077, the ratio f/α = 1.10…1.95; at α = 0.129, the ratio f/α = 1.19…1.95; at α = 0.168, the ratio f/α = 1.28…1.95.

This study’s results make it possible to solve technological problem related to the development of rolling schemes when the gripping force of friction and the pushing force of normal pressure arise during the forming process

Author Biographies

Valeriy Chigirinsky, Rudny Industrial Institute

Doctor of Technical Sciences, Professor

Department of Metallurgy and Mining

Abdrakhman Naizabekov, Rudny Industrial Institute

Doctor of Technical Sciences, Professor

Department of Metallurgy and Mining

Sergey Lezhnev, Rudny Industrial Institute

Candidate of Technical Sciences, Professor

Department of Metallurgy and Mining

Olena Naumenko, Dnipro University of Technology

Senior Lecturer

Department of Mechanical and Biomedical Engineering

Sergey Kuzmin, Rudny Industrial Institute

Candidate of Technical Sciences

Department of Metallurgy and Mining

Sergey Melentyev, Rudny Industrial Institute

Senior Lecturer

Department of Metallurgy and Mining

References

  1. Chigirinsky, V., Naizabekov, A., Lezhnev, S., Naumenko, O., Kuzmin, S. (2024). Determining the patterns of asymmetric interaction of plastic medium with counter-directional metal flow. Eastern-European Journal of Enterprise Technologies, 1 (7 (127)), 66–82. https://doi.org/10.15587/1729-4061.2024.293842
  2. Chigirinsky, V., Naizabekov, A., Lezhnev, S., Kuzmin, S., Panin, E., Tolkushkin, A. et al. (2024). Effect of the limiting deformation zone under conditions of asymmetric loading during rolling of medium thickness strips. Journal of Chemical Technology and Metallurgy, 59 (4), 993–1002. https://doi.org/10.59957/jctm.v59.i4.2024.30
  3. Chigurinski, V. V. (1999). The study of stressed and deformed metal state under conditions of nonuniform plastic medium flow. Metalurgija, 38 (1), 31–37.
  4. Chigirinsky, V., Putnoki, A. (2017). Development of a dynamic model of transients in mechanical systems using argument-functions. Eastern-European Journal of Enterprise Technologies, 3 (7 (87)), 11–22. https://doi.org/10.15587/1729-4061.2017.101282
  5. Chigirinsky, V., Naumenko, O. (2021). Advancing a generalized method for solving problems of continuum mechanics as applied to the Cartesian coordinate system. Eastern-European Journal of Enterprise Technologies, 5 (7 (113)), 14–24. https://doi.org/10.15587/1729-4061.2021.241287
  6. Chigirinsky, V., Naizabekov, A., Lezhnev, S. (2021). Closed problem of plasticity theory. Journal of Chemical Technology and Metallurgy, 56 (4), 867–876. Available at: https://journal.uctm.edu/node/j2021-4/28_21-32p867-876.pdf
  7. Chigirinsky, V., Naizabekov, A., Lezhnev, S., Kuzmin, S., Naumenko, O. (2022). Solving applied problems of elasticity theory in geomechanics using the method of argument functions of a complex variable. Eastern-European Journal of Enterprise Technologies, 5 (7 (119)), 105–113. https://doi.org/10.15587/1729-4061.2022.265673
  8. Vasyliev, L., Malich, M., Vasyliev, D., Katan, V., Rizo, Z. (2023). Improving a technique to calculate strength of cylindrical rock samples in terms of uniaxial compression. Mining of Mineral Deposits, 17 (1), 43–50. https://doi.org/10.33271/mining17.01.043
  9. Drahobetskyi, V. V., Shapoval, O. O., Shchepetov, V. V., Zahirniak, M. V., Lotous, V. V., Lehotkin, H. I. et al. (2017). Kerovani efekty plastychnoho deformuvannia zahotovok vyrobiv dlia metalurhiyi ta transportu. Kharkiv: "Drukarnia Madryd", 244. Available at: https://www.kdu.edu.ua/new/PHD_vid/KEPDZVMT.pdf
  10. Dhinwal, S. S., Toth, L. S., Lapovok, R., Hodgson, P. D. (2019). Tailoring One-Pass Asymmetric Rolling of Extra Low Carbon Steel for Shear Texture and Recrystallization. Materials, 12 (12), 1935. https://doi.org/10.3390/ma12121935
  11. Banerjee, A., Wylie, A., Da Silva, L. (2022). Near-Net Shape Manufacture of Ultra-High Strength Maraging Steel Using Flow Forming and Inertia Friction Welding: Experimental and Microstructural Characterization. Journal of Manufacturing Science and Engineering, 145 (2). https://doi.org/10.1115/1.4055519
  12. Dhinwal, S. S., Toth, L. S., Hodgson, P. D., Haldar, A. (2018). Effects of Processing Conditions on Texture and Microstructure Evolution in Extra-Low Carbon Steel during Multi-Pass Asymmetric Rolling. Materials, 11 (8), 1327. https://doi.org/10.3390/ma11081327
  13. Nadai, A. (1954). Theory of low and fracture of solids. IL Publ., New York.
  14. Timoshenko, S. P., Goodier, J. N. (1952). Theory of Elasticity. Timoshenkoand Goodier . McGraw-Hill. New York 1951. 493 pp. 270 diagrams. 81s. net. (New Edition.). The Journal of the Royal Aeronautical Society, 56 (496), 308–308. https://doi.org/10.1017/s036839310012471x
  15. Dorofeyev, O. A., Kovtun, V. V. (2019). Estimation of the Stress-Strain State of a Discrete Medium by a Plastic Flow Model. PROBLEMS OF TRIBOLOGY, 93 (3), 29–38. https://doi.org/10.31891/2079-1372-2019-93-3-29-38
  16. El-Naaman, S. A., Nielsen, K. L., Niordson, C. F. (2019). An investigation of back stress formulations under cyclic loading. Mechanics of Materials, 130, 76–87. https://doi.org/10.1016/j.mechmat.2019.01.005
  17. Lopez-Crespo, P., Camas, D., Antunes, F. V., Yates, J. R. (2018). A study of the evolution of crack tip plasticity along a crack front. Theoretical and Applied Fracture Mechanics, 98, 59–66. https://doi.org/10.1016/j.tafmec.2018.09.012
  18. Li, J., Zhang, Z., Li, C. (2017). Elastic-plastic stress-strain calculation at notch root under monotonic, uniaxial and multiaxial loadings. Theoretical and Applied Fracture Mechanics, 92, 33–46. https://doi.org/10.1016/j.tafmec.2017.05.005
  19. Pathak, H. (2017). Three-dimensional quasi-static fatigue crack growth analysis in functionally graded materials (FGMs) using coupled FE-XEFG approach. Theoretical and Applied Fracture Mechanics, 92, 59–75. https://doi.org/10.1016/j.tafmec.2017.05.010
  20. Correia, J. A. F. O., Huffman, P. J., De Jesus, A. M. P., Cicero, S., Fernández-Canteli, A., Berto, F., Glinka, G. (2017). Unified two-stage fatigue methodology based on a probabilistic damage model applied to structural details. Theoretical and Applied Fracture Mechanics, 92, 252–265. https://doi.org/10.1016/j.tafmec.2017.09.004
  21. Sneddon, I. N., Berry, D. S. (1958). The Classical Theory of Elasticity. Elasticity and Plasticity / Elastizität Und Plastizität, 1–126. https://doi.org/10.1007/978-3-642-45887-3_1
  22. Hussein, N. S. (2014). Solution of a Problem Linear Plane Elasticity with Mixed Boundary Conditions by the Method of Boundary Integrals. Mathematical Problems in Engineering, 2014 (1). https://doi.org/10.1155/2014/323178
  23. Yu, T., Xue, P. (2022). Introduction to Engineering Plasticity. Elsevier. https://doi.org/10.1016/c2021-0-00546-0
  24. Muñoz, J. A., Avalos, M., Schell, N., Brokmeier, H. G., Bolmaro, R. E. (2021). Comparison of a low carbon steel processed by Cold Rolling (CR) and Asymmetrical Rolling (ASR): Heterogeneity in strain path, texture, microstructure and mechanical properties. Journal of Manufacturing Processes, 64, 557–575. https://doi.org/10.1016/j.jmapro.2021.02.017
Identifying a mechanism for the gripping ability of rolls and rolling at a stability limit under asymmetric loading

Downloads

Published

2025-10-30

How to Cite

Chigirinsky, V., Naizabekov, A., Lezhnev, S., Naumenko, O., Kuzmin, S., & Melentyev, S. (2025). Identifying a mechanism for the gripping ability of rolls and rolling at a stability limit under asymmetric loading. Eastern-European Journal of Enterprise Technologies, 5(1 (137), 31–54. https://doi.org/10.15587/1729-4061.2025.340835

Issue

Vol. 5 No. 1 (137) (2025): Engineering technological systems

Section

Engineering technological systems

License

Copyright (c) 2025 Valeriy Chigirinsky, Abdrakhman Naizabekov, Sergey Lezhnev, Olena Naumenko, Sergey Kuzmin, Sergey Melentyev

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.