Підхід до синтезу аперіодичної робастної системи автоматичного керування на основі градієнтно-швидкісного методу вектор-функцій Ляпунова
DOI:
https://doi.org/10.15587/1729-4061.2023.274063Ключові слова:
робастна стійкість, лінійні багатовимірні системи, вектор-функції Ляпунова, аперіодичні робастно стійкі системиАнотація
Однією з актуальних проблем теорії та практики керування динамічними об’єктами є розробка методів дослідження та синтезу систем керування багатовимірними об’єктами.
У статті запропоновано універсальний підхід до побудови вектор-функцій Ляпунова безпосередньо з рівняння стану системи керування та новий градієнтно-швидкісний метод вектор-функцій Ляпунова для дослідження аперіодичної робастної стійкості лінійної системи керування з m входами та n виходами.
Дослідження аперіодичної робастної стійкості систем автоматичного керування базується на побудові вектор-функцій Ляпунова та градієнтно-швидкісних систем динамічного керування.
Використано основні положення теореми Ляпунова про асимптотичну стійкість та поняття стійкості динамічних систем. Представлення систем керування як градієнтних систем і функцій Ляпунова, як потенційних функцій градієнтних систем з теорії катастроф, дозволяє побудувати повну похідну векторних функцій Ляпунова завжди як знаконегативну функцію, що дорівнює скалярному добутку вектора швидкості на вектор градієнта. Отримано умови аперіодичної робастної стійкості як систему нерівностей щодо невизначених параметрів системи автоматичного керування, які є умовою існування вектор-функції Ляпунова.
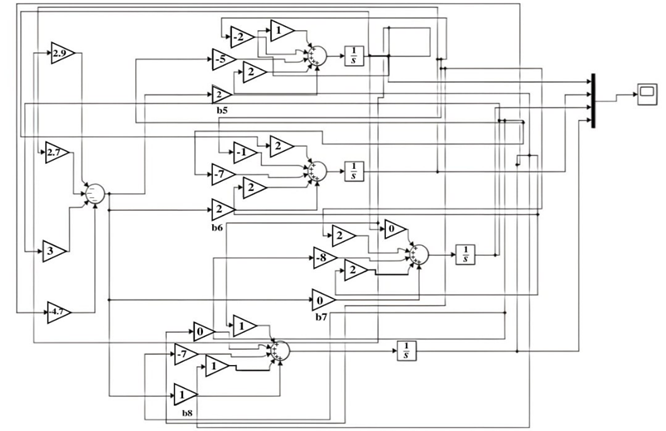
Наведено числовий приклад синтезу аперіодичної стійкості багатовимірного об'єкта керування. На прикладі показано основні етапи розробленого методу синтезу, дослідження стійкості системи при різних значеннях коефіцієнтів k, що підтверджує постійність запропонованого методу. Перехідні процеси в системі задовольняють усім вимогам
Посилання
- Beisenbi, M., Kaliyeva, S., Sagymbay, A., Abdugulova, Z., Ostayeva, A. (2021). A new approach for synthesis of the control system by gradient-velocity method of Lyapunov vector functions. Journal of Theoretical and Applied Information Technology, 2 (99), 381–389. Available at: http://www.jatit.org/volumes/Vol99No2/11Vol99No2.pdf
- Chen, H.-G., Han, K.-W. (1997). Robust Controller Design with Damping and Stability Specifications. Journal of Guidance, Control, and Dynamics, 20 (2), 400–403. doi: https://doi.org/10.2514/2.4055
- Chen, H.-G., Han, K.-W. (1993). Stability-robustness analysis for linear systems with state-space models. Journal of the Franklin Institute, 330 (5), 939–966. doi: https://doi.org/10.1016/0016-0032(93)90087-b
- Barbashin, E. A. (1967). Introduction in the theory of stability. Moscow: Nauka.
- Andreev, Y. N. (1976). Control of finite dimensional linear objects. Moscow: Nauka.
- Bailey, F. N. (1965). The Application of Lyapunov’s Second Method to Interconnected Systems. Journal of the Society for Industrial and Applied Mathematics Series A Control, 3 (3), 443–462. doi: https://doi.org/10.1137/0303030
- Beisenbi, M., Uskenbayeva, G. (2014). The New Approach of Design Robust Stability for Linear Control System. Proceedings of the International Conference on Advances in Electronics and Electrical Technology, Institute of Research engineers and Doctors. Bangkok, 11–18.
- Kuznetsov, N. V. (2020). Theory of Hidden Oscillations and Stability of Control Systems. Journal of Computer and Systems Sciences International, 59 (5), 647–668. doi: https://doi.org/10.1134/s1064230720050093
- Petridis, V., Petridis, S. (2006). Construction of Neural Network Based Lyapunov Functions. The 2006 IEEE International Joint Conference on Neural Network Proceedings. doi: https://doi.org/10.1109/ijcnn.2006.247233
- Parkhomenko, L., Butko, T., Prokhorov, V., Kalashnikova, T., Golovko, T. (2022). Building a model for planning rapid delivery of containers by rail under the conditions of intermodal transportation based on robust optimization. Eastern-European Journal of Enterprise Technologies, 5 (3 (119)), 6–16. doi: https://doi.org/10.15587/1729-4061.2022.265668
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2023 Мamyrbek Beisenbi, Samal Kaliyeva

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.
Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.









