Construction of a physical-mathematical model of oscillations of the unbalanced vibrator of the pneumatic sorting table
DOI:
https://doi.org/10.15587/1729-4061.2023.281425Keywords:
unbalanced vibrator, pneumatic sorting table, oscillation of a round plate, dynamic effect of asymmetryAbstract
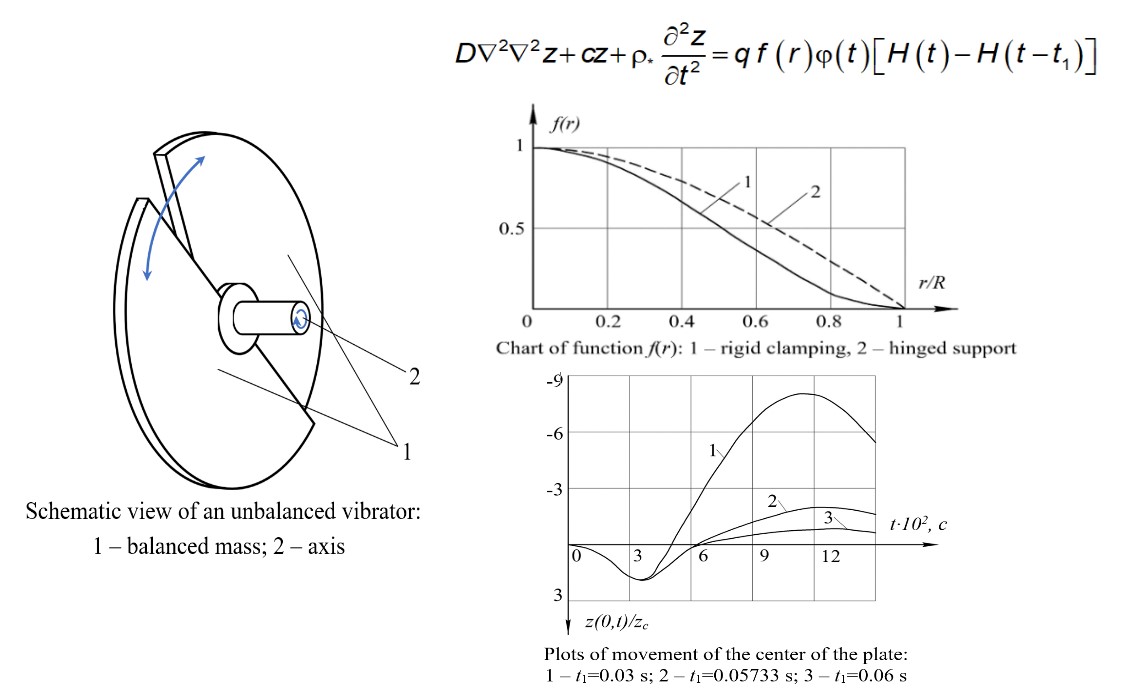
A physical-mathematical model of oscillations of unbalanced vibrators of a pneumatic sorting table as non-stationary oscillations of an impulse-loaded round plate with various options for fixing its contour has been built. The axisymmetric non-stationary oscillations of a round plate supported by a one-sided round base were considered in two ways of fixing its contour, namely, when it is tightly clamped and freely supported. It was assumed that the linearly elastic base resists only compression and does not perceive stretching. It is shown that for certain durations of the transverse force pulse in time, the amplitude of the deflection of the middle of the plate in the direction of action of the external pulse can be smaller than the amplitude of the deflection in the opposite direction. At the same time, in the second case, there is no contact of the plate with the base. It has been proven that this dynamic effect of the asymmetry of the elastic characteristic of the system also applies to bending moments and is more clearly manifested when the contour is freely supported than when it is tightly clamped. For rectangular and sinusoidal pulses, closed-loop solutions of the equations of motion of the plate during its contact with the base and after separation from the base were constructed. Compact formulas were derived for calculating the amplitudes of positive and negative deflections in both directions from the zero position of static equilibrium. Formulas have been obtained for calculating the time it takes for the plate to obtain extreme deflection values, which is achieved due to the selection of a special axisymmetric distribution of dynamic pressure on the plate. Under such a load, the plate simultaneously detaches from the base at all points, except for the contour points, which reduces the nonlinear boundary value problem to a sequence of two linear problems. Numerical integration of the differential equation was carried out to check the reliability of the constructed analytical solutions. Adequacy of the model was proven for the following values of initial parameters: modulus of elasticity, 2.1·1011 Pa; the Poisson ratio of the plate material, 0.25; plate thickness, 7...10 mm; the maximum pressure on the plate, 4·103 Pa; the bending stiffness of the plate, 6402.6667 N·m
References
- Yang, B. (2019). Machine learning-based evolution model and the simulation of a profit model of agricultural products logistics financing. Neural Computing and Applications, 31 (9), 4733–4759. doi: https://doi.org/10.1007/s00521-019-04072-5
- Adamchuk, V., Bulgakov, V., Ivanovs, S., Holovach, I., Ihnatiev, Y. (2021). Theoretical study of pneumatic separation of grain mixtures in vortex flow. Engineering for Rural Development. doi: https://doi.org/10.22616/erdev.2021.20.tf139
- Kharchenko, S., Borshch, Y., Kovalyshyn, S., Piven, M., Abduev, M., Miernik, A. et al. (2021). Modeling of Aerodynamic Separation of Preliminarily Stratified Grain Mixture in Vertical Pneumatic Separation Duct. Applied Sciences, 11 (10), 4383. doi: https://doi.org/10.3390/app11104383
- Bulgakov, V., Nikolaenko, S., Holovach, I., Boris, A., Kiurchev, S., Ihnatiev, Y., Olt, J. (2020). Theory of motion of grain mixture particle in the process of aspiration separation. Agronomy Research, 18 (2), 1177–1188. doi: https://doi.org/10.15159/AR.20.069
- PM 3/78 (2) Consignment inspection of seed and grain of cereals. (2021). EPPO Bulletin, 51 (3), 387–396. doi: https://doi.org/10.1111/epp.12772
- Bredykhin, V., Gurskyi, P., Alfyorov, O., Bredykhina, K., Pak, A. (2021). Improving the mechanical-mathematical model of grain mass separation in a fluidized bed. Eastern-European Journal of Enterprise Technologies, 3 (1 (111)), 79–86. doi: https://doi.org/10.15587/1729-4061.2021.232017
- Manevich, A. I. (2020). Stability of synchronous regimes in unbalanced rotors on elastic base. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 235 (20), 4735–4748. doi: https://doi.org/10.1177/0954406220920325
- Dreizler, R. M., Lüdde, C. S. (2010). Dynamics I: Axioms and Conservation Laws. Graduate Texts in Physics, 67–137. doi: https://doi.org/10.1007/978-3-642-11138-9_3
- Smetankina, N., Merkulova, A., Merkulov, D., Postnyi, O. (2021). Dynamic Response of Laminate Composite Shells with Complex Shape Under Low-Velocity Impact. Integrated Computer Technologies in Mechanical Engineering - 2020, 267–276. doi: https://doi.org/10.1007/978-3-030-66717-7_22
- Hu, Y.-T., Huang, Y.-Y., Li, S.-P., Zhong, W.-F. (1999). The effects of bridging in a 3D composite on buckling, postbuckling and growth of delamination. Archive of Applied Mechanics (Ingenieur Archiv), 69 (6), 419–428. doi: https://doi.org/10.1007/s004190050231
- Akavci, S. S., Yerli, H. R., Dogan, A. (2007). The first order shear deformation theory for symmetrically laminated composite plates on elastic foundation. The Arabian journal for science and engineering, 32 (2B), 341–348. Available at: https://www.researchgate.net/publication/288690011_The_first_order_shear_deformation_theory_for_symmetrically_laminated_composite_plates_on_elastic_foundation
- Birman, V. (2008). Shape memory elastic foundation and supports for passive vibration control of composite plates. International Journal of Solids and Structures, 45 (1), 320–335. doi: https://doi.org/10.1016/j.ijsolstr.2007.08.023
- Popov, V., Kyrylova, O. (2020). A Dynamic Contact Problem of Torsion that Reduces to the Singular Integral Equation with Two Fixed Singularities. Proceedings of the Third International Conference on Theoretical, Applied and Experimental Mechanics, 187–192. doi: https://doi.org/10.1007/978-3-030-47883-4_35
- Zenkour, A. M. (2011). Bending of orthotropic plates resting on Pasternak’s foundations using mixed shear deformation theory. Acta Mechanica Sinica, 27 (6), 956–962. doi: https://doi.org/10.1007/s10409-011-0515-z
- Ugrimov, S., Tormosov, Yu., Kutsenko, V., Lebedinetc, I. (2014). Modeling of the stress-strain state of layered orthotropic plates on elastic foundation. Eastern-European Journal of Enterprise Technologies, 5 (7 (71)), 4–9. doi: https://doi.org/10.15587/1729-4061.2014.27632
- Dehghany, M., Farajpour, A. (2014). Free vibration of simply supported rectangular plates on Pasternak foundation: An exact and three-dimensional solution. Engineering Solid Mechanics, 2 (1), 29–42. doi: https://doi.org/10.5267/j.esm.2013.12.001
- Setooden, A., Azizi, A. (2015). Bending and free vibration analyses of rectangular laminated composite plates resting on elastic foundation using a refined shear deformation theory. Iranian Journal of Materials Forming, 2 (2), 1–13. doi: https://doi.org/10.22099/ijmf.2015.3236
- Zenkour, A. M., Radwan, A. F. (2019). Hygrothermo-mechanical buckling of FGM plates resting on elastic foundations using a quasi-3D model. International Journal for Computational Methods in Engineering Science and Mechanics, 20 (2), 85–98. doi: https://doi.org/10.1080/15502287.2019.1568618
- Olshanskii, V., Olshanskii, S. (2018). On the effect of non-symmetry of the powerful characteristics of the vibration system in mechanical impact. Vibratsiyi v tekhnitsi ta tekhnolohiyakh, 2, 36–40. Available at: http://nbuv.gov.ua/UJRN/vvtt_2018_2_7
- Olshanskiy, V., Slipchenko, M. (2021). Dynamic effect of asymmetry in oscillating systems. InterConf, 50. Available at: https://ojs.ukrlogos.in.ua/index.php/interconf/article/view/11463
- Yatsun, V., Filimonikhina, I., Podoprygora, N., Hurievska, O. (2018). Motion equations of the singlemass vibratory machine with a rotaryoscillatory motion of the platform and a vibration exciter in the form of a passive autobalancer. Eastern-European Journal of Enterprise Technologies, 6 (7 (96)), 58–67. doi: https://doi.org/10.15587/1729-4061.2018.150339
- Ol’shanskii, V. P., Burlaka, V. V., Slipchenko, M. V. (2019). Dynamics of Impulse-Loaded Beam with One-Sided Support Ties. International Applied Mechanics, 55 (5), 575–583. doi: https://doi.org/10.1007/s10778-019-00979-7
- Jung, D. (2018). Supercritical Coexistence Behavior of Coupled Oscillating Planar Eccentric Rotor/Autobalancer System. Shock and Vibration, 2018, 1–19. doi: https://doi.org/10.1155/2018/4083897
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2023 Maksym Slipchenko, Vadym Bredykhin, Liliia Kis-Korkishchenko, Andrey Pak, Oleksiy Alfyorov

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.








