Constructing geometrical models of spherical analogs of the involute of a circle and cycloid
DOI:
https://doi.org/10.15587/1729-4061.2023.284982Keywords:
involute, cycloid, spatial curves, parametric equations, geometric model, spherical analogsAbstract
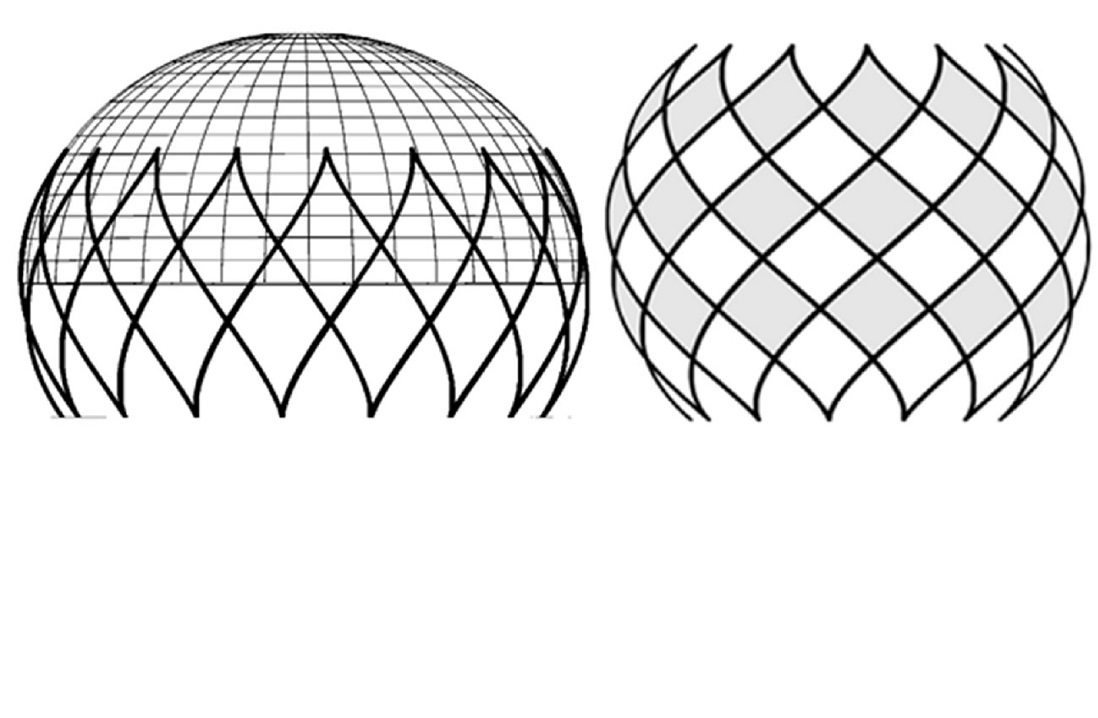
The common properties of images on a plane and a sphere are considered in the scientific works by scientists-designers of spherical mechanisms. This is due to the fact that the plane and the sphere share common geometric parameters. They include constancy at all points of the Gaussian curve, which has a zero value for a plane and a positive value for a sphere. Figures belonging to them can slide freely on both surfaces. With unlimited growth of the radius of the sphere, its limited section approaches the plane, and the spherical shape transforms into a plane. Thus, a loxodrome that crosses all meridians at a constant angle is transformed into a logarithmic spiral that intersects at a constant angle the radius vectors that come from the pole. The tooth profile of cylindrical gears is outlined by the involute of a circle. A spherical involute is used for the corresponding bevel gears. Other spherical curves are also known, which are analogs of flat ones.
The formation of a cycloid and an involute of a circle are associated with the mutual rolling of a line segment with each of these figures. If the segment is fixed and the circle rolls along it, then the point of the circle describes the cycloid. In the case of a stationary circle along which a segment is rolled, the point of the segment will execute the involute. To move to the spherical analogs of these curves, it is necessary to replace the circle with a cone, and the straight line with a plane. The spherical prototype of the cycloid will be the trajectory of the point of the base of the cone, which rolls along the plane, that is, along the sweep of the cone. The sweep of a cone is a sector, the radius of the limiting circle of which is equal to the generating cone. If this sweep, like a section of a plane, is rolled around a fixed cone, when its top coincides with the center of the sector, then the point of the limiting radius of the sector will execute a spherical involute. This paper analytically implements these two motions and reports the parametric equations of the spherical analogs of the circle involute and the cycloid
References
- Xiao, D., Prior, C. B., Yeates, A. R. (2023). Spherical winding and helicity. Journal of Physics A: Mathematical and Theoretical, 56 (20), 205201. doi: https://doi.org/10.1088/1751-8121/accc17
- Castro, I., Castro-Infantes, I., Castro-Infantes, J. (2021). Spherical curves whose curvature depends on distance to a great circle. arXiv. doi: https://doi.org/10.48550/arXiv.2111.00458
- Yuksel, N., Karacan, M. K., Demirkıran, T. (2022). Spherical Curves with Modified Orthogonal Frame with Torsion. Turkish Journal of Science, 7 (3), 177–184. Available at: https://dergipark.org.tr/tr/download/article-file/2505753
- Wang, Y., Chang, Y. (2020). Mannheim curves and spherical curves. International Journal of Geometric Methods in Modern Physics, 17 (07), 2050101. doi: https://doi.org/10.1142/s0219887820501017
- Balki-Okullu, P., Kocayigit, H., Agirman-Aydin, T. (2019). An explicit characterization of spherical curves according to bishop frame and an approximately solution. Thermal Science, 23, 361–370. doi: https://doi.org/10.2298/tsci181101049b
- Kresan, T., Pylypaka, S., Ruzhylo, Z., Rogovskii, C., Trokhaniak, O. (2022). Construction of conical axoids on the basis of congruent spherical ellipses. Archives of Materials Science and Engineering, 113 (1), 13–18. doi: https://doi.org/10.5604/01.3001.0015.6967
- Pylypaka, S. F., Hryshchenko, I. Yu., Nesvidomyna, O. V. (2018). Konstruiuvannia izometrychnykh sitok na poverkhni kuli. Prykladna heometriya ta inzhenerna hrafika, 94, 82–87. Available at: http://nbuv.gov.ua/UJRN/prgeoig_2018_94_16
- Pylypaka, S. F., Grischenko, I. Yu., Kresan, T. A. (2018). Modelling of bands of unrolled surfaces, tangential to the sphere surface. Prykladni pytannia matematychnoho modeliuvannia, 1, 81–88. Available at: http://nbuv.gov.ua/UJRN/apqmm_2018_1_10
- Novoe v systeme Mathematica 13. Available at: https://www.wolfram.com/mathematica/new-in-13/?src=google&416&gclid=CjwKCAjwoIqhBhAGEiwArXT7K8zKs9Z8YovGKAWvKBp7u47bBVWpdVSzgJKfFc9pm5A6bmMfWlUH1hoCu1cQAvD_BwE
- Maple. Available at: https://www.maplesoft.com/products/Maple/
- Berezin, V. (1978). Sfericheskiy ellips. Kvant, 2, 25.
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2023 Andrii Nesvidomin, Serhii Pylypaka, Tatiana Volina, Mykhailo Kalenyk, Ivan Shuliak, Yuriy Semirnenko, Nataliia Tarelnyk, Iryna Hryshchenko, Yuliia Kholodniak, Larysa Sierykh

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.








