Development of the method of general interpolation for Z-number-valued if-then rules
DOI:
https://doi.org/10.15587/1729-4061.2023.286164Keywords:
Z-number, fuzzy number, partial reliability, if-then rules, interpolation, distance, weightsAbstract
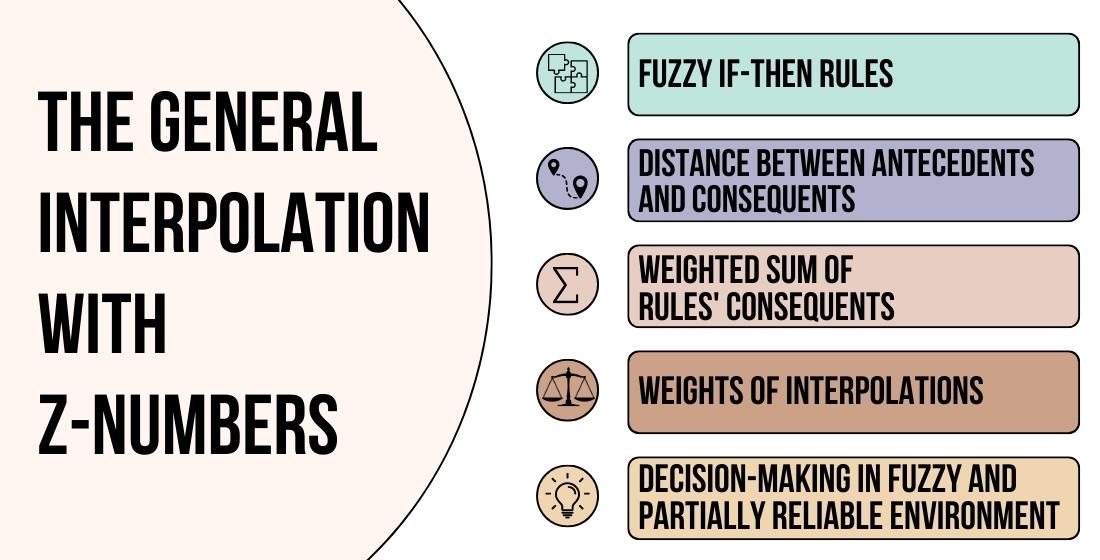
Rule interpolation-based methods are used when the rule base is sparse. This frequently being the case, as information relevant to real-world problems is not usually comprehensive. At the same time, relevant information is often characterized by both fuzziness and partial reliability. To deal with such kind of information, the concept of Z-number was introduced by Zadeh. This paper is devoted to an extension of the general interpolation method for fuzzy rules to the case of if-then rules with Z-number-valued antecedents and consequents. The proposed approach relies on the determination of the distance between the current observation vector and vectors of rules antecedents. By determining the distance between the current vector and the antecedents of the rules, decisions can be made based on the nearest antecedents. In this context, rule antecedents are vectors that represent certain conditions. The resulting output is computed as a weighted sum of rules consequents. Weighting factors are used to account for the importance of each rule in the interpolation. Weights of interpolations are found on the basis of mentioned distance values. The results of this study are aimed at developing an approach to decision-making in terms of Z-valued information. The method is characterized by relatively low computational complexith. Regarding the application of the proposed approach, the job satisfaction evaluation problem is considered. Consequently, the obtained results confirm the efficiency of the proposed approach. The proposed method can be a useful tool for decision-making in various applications, especially where high computational complexity is unacceptable or impractical
References
- Zadeh, L. A. (2011). A Note on Z-numbers. Information Sciences, 181 (14), 2923–2932. doi: https://doi.org/10.1016/j.ins.2011.02.022
- Chen, S.-M., Chang, Y.-C. (2011). Fuzzy rule interpolation based on interval type-2 Gaussian fuzzy sets and genetic algorithms. 2011 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2011). doi: https://doi.org/10.1109/fuzzy.2011.6007533
- Huang, Z. (2006). Rule Model Simplification. University of Edinburgh. Available at: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=fb72b35e95303843a5c4f661ca162c65678a4a65
- Li, F., Shang, C., Li, Y., Yang, J., Shen, Q. (2021). Approximate reasoning with fuzzy rule interpolation: background and recent advances. Artificial Intelligence Review, 54 (6), 4543–4590. doi: https://doi.org/10.1007/s10462-021-10005-3
- Alzubi, M., Johanyák, Z. C., Kovács, Sz. (2018). Fuzzy Rule Interpolation Methods and Fri Toolbox. Journal of Theoretical and Applied Information Technology, 96 (21). Available at: https://www.researchgate.net/publication/329239835_FUZZY_RULE_INTERPOLATION_METHODS_AND_FRI_TOOLBOX
- Naik, N., Diao, R Shen, Q. (2018). Dynamic Fuzzy Rule Interpolation and Its Application to Intrusion Detection. IEEE Transactions on Fuzzy Systems, 26 (4), 1878–1892. doi: https://doi.org/10.1109/tfuzz.2017.2755000
- Das, S., Chakraborty, D., Kóczy, L. T. (2019). Linear fuzzy rule base interpolation using fuzzy geometry. International Journal of Approximate Reasoning, 112, 105–118. doi: https://doi.org/10.1016/j.ijar.2019.05.004
- Tikk, D., Johanyák, Z. C., Kovács, S., Wong, K. W. (2011). Fuzzy Rule Interpolation and Extrapolation Techniques: Criteria and Evaluation Guidelines. Journal of Advanced Computational Intelligence and Intelligent Informatics, 15 (3), 254–263. doi: https://doi.org/10.20965/jaciii.2011.p0254
- Chen, C., Parthaláin, N. M., Li, Y., Price, C., Quek, C., Shen, Q. (2016). Rough-fuzzy rule interpolation. Information Sciences, 351, 1–17. doi: https://doi.org/10.1016/j.ins.2016.02.036
- Chen, S.-M., Lee, L.-W. (2011). Fuzzy interpolative reasoning for sparse fuzzy rule-based systems based on interval type-2 fuzzy sets. Expert Systems with Applications, 38 (8), 9947–9957. doi: https://doi.org/10.1016/j.eswa.2011.02.035
- Aliev, R. A., Pedrycz, W., Huseynov, O. H., Eyupoglu, S. Z. (2017). Approximate Reasoning on a Basis of Z-number valued If-Then Rules. IEEE Transactions on Fuzzy Systems, 25 (6), 1589–1600. doi: https://doi.org/10.1109/tfuzz.2016.2612303
- Aliev, R. A., Huseynov, O. H., Zulfugarova, R. X. (2016). Z-Distance Based IF-THEN Rules. The Scientific World Journal, 2016, 1–9. doi: https://doi.org/10.1155/2016/1673537
- Aliev, R. A., Alizadeh, A. V., Huseynov, O. H. (2015). The arithmetic of discrete Z-numbers. Information Sciences, 290, 134–155. doi: https://doi.org/10.1016/j.ins.2014.08.024
- Aliev, R. A., Guirimov, B. G., Huseynov, O. H., Aliyev, R. R. (2021). Z-relation equation-based decision making. Expert Systems with Applications, 184, 115387. doi: https://doi.org/10.1016/j.eswa.2021.115387
- Alonso de la Fuente, M., Terán, P. (2023). Convergence in distribution of fuzzy random variables in L-type metrics. Fuzzy Sets and Systems, 470, 108653. doi: https://doi.org/10.1016/j.fss.2023.108653
- Abiyev, R. H., Saner, T., Eyupoglu, S., Sadikoglu, G. (2016). Measurement of Job Satisfaction Using Fuzzy Sets. Procedia Computer Science, 102, 294–301. doi: https://doi.org/10.1016/j.procs.2016.09.404
- Lepot, M., Aubin, J.-B., Clemens, F. (2017). Interpolation in Time Series: An Introductive Overview of Existing Methods, Their Performance Criteria and Uncertainty Assessment. Water, 9 (10), 796. doi: https://doi.org/10.3390/w9100796
- Alam, N. M. F. H. N. B., Ku Khalif, K. M. N., Jaini, N. I., Gegov, A. (2023). The Application of Z-Numbers in Fuzzy Decision Making: The State of the Art. Information, 14 (7), 400. doi: https://doi.org/10.3390/info14070400
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2023 Konul Jabbarova, Ulviyya Rzayeva, Aynur Jabbarova

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.








