Математична модель райдшерінгового сервісу залізничних перевезень зернових вантажів у вигляді коаліцій в іграх з перевантаженням

Автор(и)

  • Михайло Анатолійович Кравченко Український державний університет залізничного транспорту, Україна https://orcid.org/0000-0001-7445-8952
  • Андрій Володимирович Прохорченко Український державний університет залізничного транспорту, Україна https://orcid.org/0000-0003-3123-5024
  • Сергій Анатолійович Золотрьов Український державний університет залізничного транспорту, Україна https://orcid.org/0009-0001-5951-4589

DOI:

https://doi.org/10.15587/1729-4061.2023.289470

Ключові слова:

Rail freight, перевезення зерна, райдшерінг, коаліційні ігри, ігри з перевантаженням, congestion game

Анотація

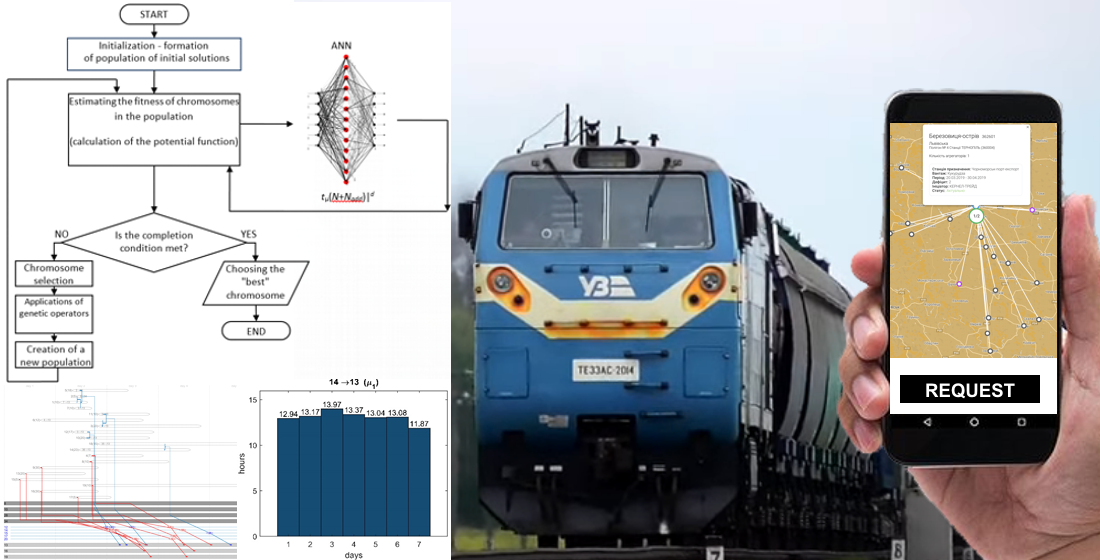
Об’єктом дослідження є процеси перевезень зернових вантажів на основі принципів райдшерінгу в залізничних системах без дотримання розкладу руху для вантажних поїздів. Для дослідження впливу моделі залізничних перевезень зерна за принципами спільного використання на роботу залізничної системи, запропоновано формалізувати даний процес в умовах пікового періоду навантаження. Перевезення зерна з використанням райдшерінгового сервісу запропоновано формалізувати у вигляді коаліцій в іграх з перевантаженням. Постановку гри запропоновано перетворити на задачу нелінійної оптимізації.

В рамках дослідження проведено математичне моделювання райдшерінгового сервісу залізничних перевезень зернових вантажів. Доведена адекватність математичної моделі. Встановлено, що дотримання розкладу руху призводить до збільшення непродуктивних простоїв вагонів після навантаження, що зменшує стимули до утворення коаліцій вантажовідправниками. Однак за результатами моделювання в умовах руху за розкладом з урахуванням координації вантажовідправників та перевізника значно покращуються показники перевезення. Це стимулює вантажовідправників до утворення коаліцій. Виявлено, що середня тривалість перевезення відправки зменшилась на 14,9 % від показника за сценарієм діючої моделі перевезень – без дотримання розкладу.

Особливість отриманих результатів в рамках дослідження полягає у тому, що запропонована математична модель дозволяє адекватно змоделювати райдшерінговий сервіс перевезень зерна в залізничній системі.

Сферою практичного застосування результатів є залізнична галузь. Умовами практичного застосування результатів дослідження є важливість впровадження цифрових платформ агрегаторів для координації вантажовідправників та перевізника.

Проведені дослідження сприятимуть створенню напрацювань щодо удосконалення зернової логістики на залізничному транспорті

Біографії авторів

Михайло Анатолійович Кравченко, Український державний університет залізничного транспорту

Аспірант

Кафедра управління експлуатаційною роботою

Андрій Володимирович Прохорченко, Український державний університет залізничного транспорту

Доктор технічних наук, професор

Кафедра управління експлуатаційною роботою

Сергій Анатолійович Золотрьов, Український державний університет залізничного транспорту

Аспірант

Кафедра управління експлуатаційною роботою

Посилання

  1. Prokhorchenko, А., Kravchenko, M., Prokopov, A. (2021). Improvement of railway logistics of grain cargo on the basis principles of ridesharing. Thesis of XIII international scientific and practical conference: Globalization of scientific and educational space. Innovations of transport. Problems, experience, prospects. Vlora, 63. Available at: https://dspace.snu.edu.ua/server/api/core/bitstreams/4214928a-49d3-40a7-8cd7-212b933c11c1/content
  2. Zagurskiy, O., Savchenko, L., Makhmudov, I., Matsiuk, V. (2022). Assessment of socio-ecological efficiency of transport and logistics activity. Engineering for Rural Development. doi: https://doi.org/10.22616/erdev.2022.21.tf182
  3. Jeong, S.-J., Lee, C.-G., Bookbinder, J. H. (2007). The European freight railway system as a hub-and-spoke network. Transportation Research Part A: Policy and Practice, 41 (6), 523–536. doi: https://doi.org/10.1016/j.tra.2006.11.005
  4. Irina, T., Moroz, M., Zahorianskyi, V., Zahorianskaya, O., Moroz, O. (2021). Management of the Logistics Component of the Grain HarvestingProcess with Consideration of the Choice of Automobile Transport Technology Based on the Energetic Criterion. 2021 IEEE International Conference on Modern Electrical and Energy Systems (MEES). doi: https://doi.org/10.1109/mees52427.2021.9598768
  5. Butko, T., Prokhorov, V., Kalashnikova, T., Riabushka, Y. (2019). Organization of railway freight short-haul transportation on the basis of logistic approaches. Procedia Computer Science, 149, 102–109. doi: https://doi.org/10.1016/j.procs.2019.01.113
  6. Poriadok napravlennia vahonopotokiv i orhanizatsiyi yikh u vantazhni poizdy na 2021–2022 roky (plan formuvannia poizdiv). Ofitsiynyi sait AT Ukrzaliznytsia. Available at: https://www.uz.gov.ua/cargo_transportation/general_information/formuvannia/
  7. Carissimi, M. C., Creazza, A. (2022). The role of the enabler in sharing economy service triads: A logistics perspective. Cleaner Logistics and Supply Chain, 5, 100077. doi: https://doi.org/10.1016/j.clscn.2022.100077
  8. Chan, N. D., Shaheen, S. A. (2012). Ridesharing in North America: Past, Present, and Future. Transport Reviews, 32 (1), 93–112. doi: https://doi.org/10.1080/01441647.2011.621557
  9. A Flapper permite fretar jatos executivos e comprar assentos em voos compartilhados. Tudo pelo app (2019). Available at: https://www.projetodraft.com/a-flapper-permite-fretar-jatos-executivos-e-comprar-assentos-em-voos-compartilhados-tudo-pelo-app/
  10. Yao, R., Bekhor, S. (2022). A ridesharing simulation model that considers dynamic supply-demand interactions. Journal of Intelligent Transportation Systems, 1–23. doi: https://doi.org/10.1080/15472450.2022.2098730
  11. Pouls, M., Ahuja, N., Glock, K., Meyer, A. (2022). Adaptive forecast-driven repositioning for dynamic ride-sharing. Annals of Operations Research. doi: https://doi.org/10.1007/s10479-022-04560-3
  12. Zhang, H., Zhao, J. (2019). Mobility Sharing as a Preference Matching Problem. IEEE Transactions on Intelligent Transportation Systems, 20 (7), 2584–2592. doi: https://doi.org/10.1109/tits.2018.2868366
  13. Altshuler, T., Altshuler, Y., Katoshevski, R., Shiftan, Y. (2019). Modeling and Prediction of Ride-Sharing Utilization Dynamics. Journal of Advanced Transportation, 2019, 1–18. doi: https://doi.org/10.1155/2019/6125798
  14. Campbell, I., Ali, M. M., Fienberg, M. L. (2016). Solving the dial-a-ride problem using agent- based simulation. South African Journal of Industrial Engineering, 27 (3). doi: https://doi.org/10.7166/27-3-1649
  15. Tellez, O., Vercraene, S. V., Lehuédé, F., Péton, O., Monteiro, T. (2017). Diala-ride problem for disabled people using vehicles with reconfigurable capacity. 20th IFAC World Congress of the International Federation of Automatic Control (IFAC 2017). Toulouse. Available at: https://hal.science/hal-01760353/document
  16. Cordeau, J.-F., Laporte, G. (2007). The dial-a-ride problem: models and algorithms. Annals of Operations Research, 153 (1), 29–46. doi: https://doi.org/10.1007/s10479-007-0170-8
  17. Ma, T.-Y., Rasulkhani, S., Chow, J. Y. J., Klein, S. (2019). A dynamic ridesharing dispatch and idle vehicle repositioning strategy with integrated transit transfers. Transportation Research Part E: Logistics and Transportation Review, 128, 417–442. doi: https://doi.org/10.1016/j.tre.2019.07.002
  18. Mahmoudi, M., Chen, J., Shi, T., Zhang, Y., Zhou, X. (2019). A cumulative service state representation for the pickup and delivery problem with transfers. Transportation Research Part B: Methodological, 129, 351–380. doi: https://doi.org/10.1016/j.trb.2019.09.015
  19. Ghilas, V., Demir, E., Van Woensel, T. (2016). The pickup and delivery problem with time windows and scheduled lines. INFOR: Information Systems and Operational Research, 54 (2), 147–167. doi: https://doi.org/10.1080/03155986.2016.1166793
  20. Zheng, H., Zhang, X., Chen, J. (2021). Study on Customized Shuttle Transit Mode Responding to Spatiotemporal Inhomogeneous Demand in Super-Peak. Information, 12 (10), 429. doi: https://doi.org/10.3390/info12100429
  21. Bistaffa, F., Farinelli, A., Chalkiadakis, G., Ramchurn, S. D. (2017). A cooperative game-theoretic approach to the social ridesharing problem. Artificial Intelligence, 246, 86–117. doi: https://doi.org/10.1016/j.artint.2017.02.004
  22. Pandey, V., Monteil, J., Gambella, C., Simonetto, A. (2019). On the needs for MaaS platforms to handle competition in ridesharing mobility. Transportation Research Part C: Emerging Technologies, 108, 269–288. doi: https://doi.org/10.1016/j.trc.2019.09.021
  23. Singh, A., Maurya, A. K., Singh, S. P., Pandey, H., Tripathi, U. N. (2021). Cooperative game theory approaches to manage traffic congestion in wireless network*. Bulletin of Pure & Applied Sciences- Mathematics and Statistics, 40e (1), 1–13. doi: https://doi.org/10.5958/2320-3226.2021.00001.1
  24. Hayrapetyan, A., Tardos, É., Wexler, T. (2006). The effect of collusion in congestion games. Proceedings of the Thirty-Eighth Annual ACM Symposium on Theory of Computing. doi: https://doi.org/10.1145/1132516.1132529
  25. Shams, F., Luise, M. (2013). Basics of coalitional games with applications to communications and networking. EURASIP Journal on Wireless Communications and Networking, 2013 (1). doi: https://doi.org/10.1186/1687-1499-2013-201
  26. Hao, Y., Pan, S., Qiao, Y., Cheng, D. (2018). Cooperative Control via Congestion Game Approach. IEEE Transactions on Automatic Control, 63 (12), 4361–4366. doi: https://doi.org/10.1109/tac.2018.2824978
  27. 126. Game Theory. Spring 2016. Massachusetts Institute of Technology. Available at: https://ocw.mit.edu/courses/14-126-game-theory-spring-2016/resources/14-126s16/
  28. Prokhorchenko, A., Kravchenko, M., Malakhova, O., Sikonenko, G., Prokhorchenko, H. (2022). Research of the Freight Trains Movement Stability with a Network Effect. Lecture Notes in Networks and Systems, 785–794. doi: https://doi.org/10.1007/978-3-031-20141-7_70
  29. Rosenthal, R. W. (1973). A class of games possessing pure-strategy Nash equilibria. International Journal of Game Theory, 2 (1), 65–67. doi: https://doi.org/10.1007/bf01737559
  30. Gopalakrishnan, R., Marden, J. R., Wierman, A. (2014). Potential Games Are Necessary to Ensure Pure Nash Equilibria in Cost Sharing Games. Mathematics of Operations Research, 39 (4), 1252–1296. doi: https://doi.org/10.1287/moor.2014.0651
  31. Monderer, D., Shapley, L. S. (1996). Potential Games. Games and Economic Behavior, 14 (1), 124–143. doi: https://doi.org/10.1006/game.1996.0044
  32. Wright, A. H. (1991). Genetic Algorithms for Real Parameter Optimization. Foundations of Genetic Algorithms, 205–218. doi: https://doi.org/10.1016/b978-0-08-050684-5.50016-1
  33. Kerner, B. S. (1999). Congested Traffic Flow: Observations and Theory. Transportation Research Record: Journal of the Transportation Research Board, 1678 (1), 160–167. doi: https://doi.org/10.3141/1678-20
  34. Sahinidis, N. V. (2019). Mixed-integer nonlinear programming 2018. Optimization and Engineering, 20 (2), 301–306. doi: https://doi.org/10.1007/s11081-019-09438-1
  35. Deep, K., Singh, K. P., Kansal, M. L., Mohan, C. (2009). A real coded genetic algorithm for solving integer and mixed integer optimization problems. Applied Mathematics and Computation, 212 (2), 505–518. doi: https://doi.org/10.1016/j.amc.2009.02.044
  36. Ciaburro, G. (2017). MATLAB for Machine Learning: Practical examples of regression, clustering and neural networks. Packt Publishing.
  37. Zhang, J., Pourazarm, S., Cassandras, C. G., Paschalidis, I. Ch. (2018). The Price of Anarchy in Transportation Networks: Data-Driven Evaluation and Reduction Strategies. Proceedings of the IEEE, 106 (4), 538–553. doi: https://doi.org/10.1109/jproc.2018.2790405
Математична модель райдшерінгового сервісу залізничних перевезень зернових вантажів у вигляді коаліцій в іграх з перевантаженням

##submission.downloads##

Опубліковано

2023-10-31

Як цитувати

Кравченко, М. А., Прохорченко, А. В., & Золотрьов, С. А. (2023). Математична модель райдшерінгового сервісу залізничних перевезень зернових вантажів у вигляді коаліцій в іграх з перевантаженням. Eastern-European Journal of Enterprise Technologies, 5(3 (125), 35–48. https://doi.org/10.15587/1729-4061.2023.289470

Номер

Том 5 № 3 (125) (2023): Процеси управління

Розділ

Процеси управління

Ліцензія

Авторське право (c) 2023 Mykhailo Kravchenko, Andrii Prokhorchenko, Serhii Zolotarov

Creative Commons License

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.

Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.

Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.