Розробка комбінованого методу налаштування параметрів ПІ/ПІД-регуляторів для нафтогазових об’єктів

Автор(и)

  • Михайло Іванович Горбійчук Івано-Франківський національний технічний університет нафти і газу, Україна https://orcid.org/0000-0002-8586-1883
  • Михайло Зеновійович Василенчук Івано-Франківський національний технічний університет нафти і газу, Україна https://orcid.org/0009-0008-9725-052X
  • Ігор Степанович Єднак Івано-Франківський національний технічний університет нафти і газу, Україна https://orcid.org/0009-0000-9768-2404
  • Андрій Іванович Лагойда Івано-Франківський національний технічний університет нафти і газу, Україна https://orcid.org/0000-0002-0862-7786

DOI:

https://doi.org/10.15587/1729-4061.2025.322424

Ключові слова:

система керування, комбінований критерій, ПІ/ПІД-регулятор, параметри налаштування, локальний мінімум

Анотація

Об’єктом дослідження є системи автоматичного керування першого, другого і третього порядків. Основною проблемою, що досліджувалась, було забезпечення стійкості систем керування при мінімізації перерегулювання та часу регулювання.

Розроблено комбінований метод визначення параметрів налаштування ПІ/ПІД-регуляторів, який поєднує метод s-площини та узагальнений квадратичний критерій.

Метод s-площини заснований на теоремі Вієта, яка пов’язує корені характеристичного рівняння замкненої системи керування з його параметрами. Вони, в свою чергу, є функціями параметрів налаштування ПІ/ПІД-регуляторів. Шляхом вибору лівих коренів характеристичного рівняння замкненої системи на s-площині можна добитись бажаних показників якості системи керування. Корені рівняння функціонально зв’язані з параметрами ПІ/ПІД-регуляторів. Із системи алгебраїчних рівнянь, які витікають із тереми Вієта, знаходять параметри налаштування ПІ/ПІД-регуляторів як розв’язок такої системи.

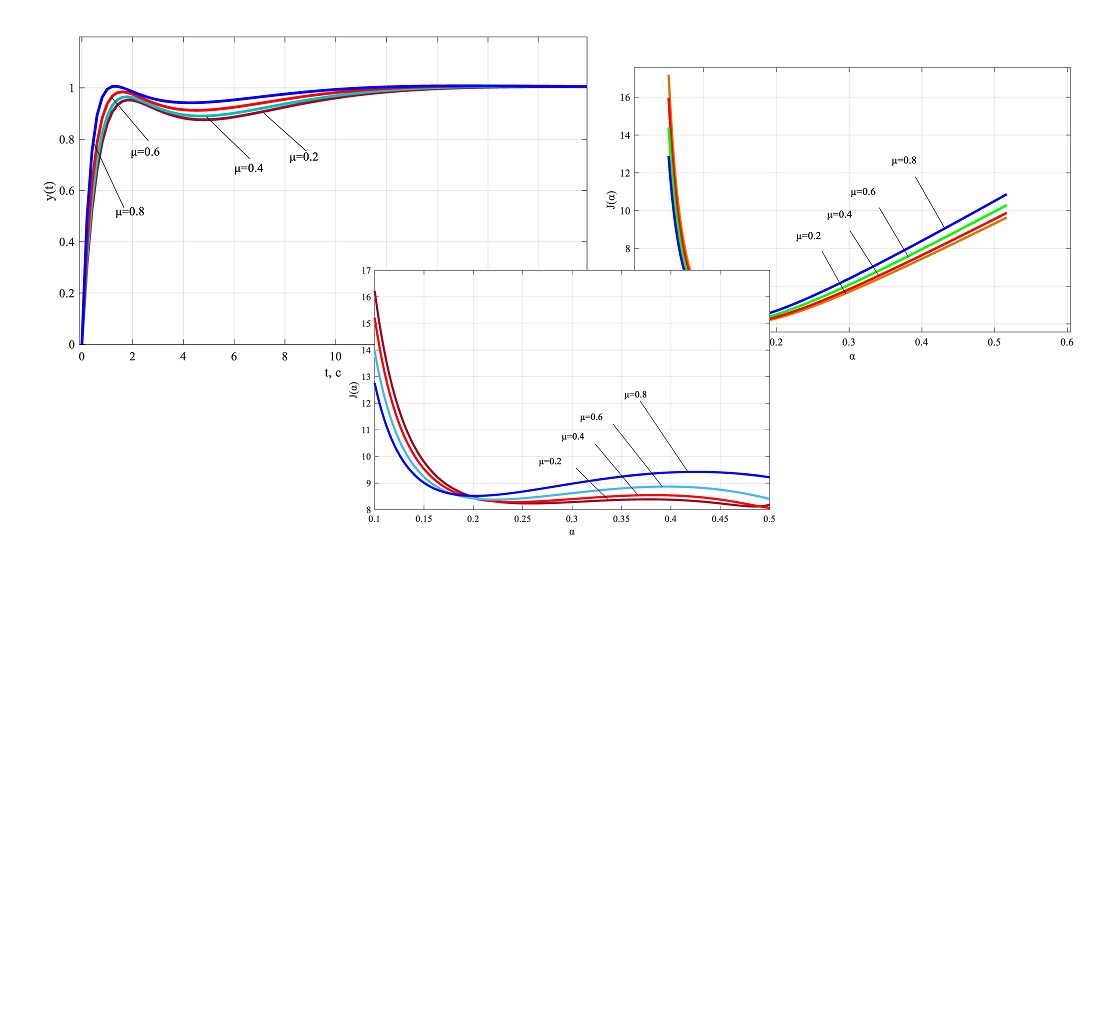
На другому етапі розв’язування задачі корені характеристичного рівняння вибирають так, щоб узагальнений квадратичний критерій був функцією тільки від дійсної частини одного із коренів характеристичного рівняння. Внаслідок цього отримали одновимірну задачу мінімізації, локальний мінімум якої шукався на заздалегідь визначеному інтервалі пошуку. Цей інтервал вибирали з умови, щоб параметри налаштування ПІ/ПІД-регуляторів були б строго додатними, а корені ж характеристичного рівняння замкненої системи належали б лівій напівплощині s-площини. Такий вибір інтервалу пошуку гарантує стійкість замкненої системи автоматичного керування.

Встановлено, що у порівнянні з методом s-площини перерегулювання і час регулювання зменшились в середньому на 73,5 % і 66,5 %. Це дозволить підвищити швидкість роботи промислових контролерів

Біографії авторів

Михайло Іванович Горбійчук, Івано-Франківський національний технічний університет нафти і газу

Доктор технічних наук

Кафедра автоматизації і комп’ютерно-інтегрованих технологій

Михайло Зеновійович Василенчук, Івано-Франківський національний технічний університет нафти і газу

Аспірант

Кафедра автоматизації і комп’ютерно-інтегрованих технологій

Ігор Степанович Єднак, Івано-Франківський національний технічний університет нафти і газу

Аспірант

Кафедра автоматизації і комп’ютерно-інтегрованих технологій

Андрій Іванович Лагойда, Івано-Франківський національний технічний університет нафти і газу

Кандидат технічних наук

Кафедра автоматизації і комп’ютерно-інтегрованих технологій

Посилання

  1. Borase, R. P., Maghade, D. K., Sondkar, S. Y., Pawar, S. N. (2020). A review of PID control, tuning methods and applications. International Journal of Dynamics and Control, 9 (2), 818–827. https://doi.org/10.1007/s40435-020-00665-4
  2. Coelho, L. dos S., Mariani, V. C. (2012). Firefly algorithm approach based on chaotic Tinkerbell map applied to multivariable PID controller tuning. Computers & Mathematics with Applications, 64 (8), 2371–2382. https://doi.org/10.1016/j.camwa.2012.05.007
  3. Kanojiya, R. G., Meshram, P. M. (2012). Optimal tuning of PI controller for speed control of DC motor drive using particle swarm optimization. 2012 International Conference on Advances in Power Conversion and Energy Technologies (APCET), 1–6. https://doi.org/10.1109/apcet.2012.6302000
  4. Ali, A., Majhi, S. (2010). PID controller tuning for integrating processes. ISA Transactions, 49 (1), 70–78. https://doi.org/10.1016/j.isatra.2009.09.001
  5. Thomsen, S., Hoffmann, N., Fuchs, F. W. (2011). PI Control, PI-Based State Space Control, and Model-Based Predictive Control for Drive Systems With Elastically Coupled Loads – A Comparative Study. IEEE Transactions on Industrial Electronics, 58 (8), 3647–3657. https://doi.org/10.1109/tie.2010.2089950
  6. Precup, R.-E., Angelov, P., Costa, B. S. J., Sayed-Mouchaweh, M. (2015). An overview on fault diagnosis and nature-inspired optimal control of industrial process applications. Computers in Industry, 74, 75–94. https://doi.org/10.1016/j.compind.2015.03.001
  7. Joseph, S. B., Dada, E. G., Abidemi, A., Oyewola, D. O., Khammas, B. M. (2022). Metaheuristic algorithms for PID controller parameters tuning: review, approaches and open problems. Heliyon, 8 (5), e09399. https://doi.org/10.1016/j.heliyon.2022.e09399
  8. Stavrov, D., Nadzinski, G., Deskovski, S., Stankovski, M. (2021). Quadratic Model-Based Dynamically Updated PID Control of CSTR System with Varying Parameters. Algorithms, 14 (2), 31. https://doi.org/10.3390/a14020031
  9. Na, S., Anitescu, M., Kolar, M. (2023). Inequality constrained stochastic nonlinear optimization via active-set sequential quadratic programming. Mathematical Programming, 202 (1-2), 279–353. https://doi.org/10.1007/s10107-023-01935-7
  10. Jayachitra, A., Vinodha, R. (2014). Genetic Algorithm Based PID Controller Tuning Approach for Continuous Stirred Tank Reactor. Advances in Artificial Intelligence, 2014, 1–8. https://doi.org/10.1155/2014/791230
  11. Saad, M. S., Jamaluddin, H., Darus, I. Z. M. (2012). Implementation of PID Controller tuning using Differential Evolution and Genetic Algorithms. Computing, Information and Control, 8 (11). Available at: https://www.researchgate.net/profile/Jyotindra-Narayan/post/How-to-tune-PID-gains-in-control-algorithm-using-particle-swarm-optimization-or-genetic-algorithm-to-minimize-the-robot-trajectory-tracking-errors/attachment/5ef2cf493f8af70001ebe5b1/AS%3A905800520318976%401592971081601/download/Implementation_of_PID_controller_tuning.pdf
  12. Cao, F. (2018). PID controller optimized by genetic algorithm for direct-drive servo system. Neural Computing and Applications, 32 (1), 23–30. https://doi.org/10.1007/s00521-018-3739-z
  13. Solihin, M. I., Tack, L. F., Kean, M. L. (2011). Tuning of PID Controller Using Particle Swarm Optimization (PSO). Proceeding of the International Conference on Advanced Science, Engineering and Information Technology. Available at: https://www.researchgate.net/profile/Lip-Kean-Moey/publication/251442573_Tuning_of_PID_Controller_Using_Particle_Swarm_Optimization_PSO/links/5b1f1d60458515270fc475db/Tuning-of-PID-Controller-Using-Particle-Swarm-Optimization-PSO.pdf
  14. Wang, D., Tan, D., Liu, L. (2017). Particle swarm optimization algorithm: an overview. Soft Computing, 22 (2), 387–408. https://doi.org/10.1007/s00500-016-2474-6
  15. Ribeiro, J. M. S., Santos, M. F., Carmo, M. J., Silva, M. F. (2017). Comparison of PID controller tuning methods: analytical/classical techniques versus optimization algorithms. 2017 18th International Carpathian Control Conference (ICCC), 533–538. https://doi.org/10.1109/carpathiancc.2017.7970458
  16. Li, S., Wei, Y., Liu, X., Zhu, H., Yu, Z. (2022). A New Fast Ant Colony Optimization Algorithm: The Saltatory Evolution Ant Colony Optimization Algorithm. Mathematics, 10 (6), 925. https://doi.org/10.3390/math10060925
  17. Niu, B., Wang, H. (2012). Bacterial Colony Optimization. Discrete Dynamics in Nature and Society, 2012 (1). https://doi.org/10.1155/2012/698057
  18. Sagban, R., Marhoon, H. A., Alubady, R. (2020). Hybrid bat-ant colony optimization algorithm for rule-based feature selection in health care. International Journal of Electrical and Computer Engineering (IJECE), 10 (6), 6655–6663. https://doi.org/10.11591/ijece.v10i6.pp6655-6663
  19. Shami, T. M., El-Saleh, A. A., Alswaitti, M., Al-Tashi, Q., Summakieh, M. A., Mirjalili, S. (2022). Particle Swarm Optimization: A Comprehensive Survey. IEEE Access, 10, 10031–10061. https://doi.org/10.1109/access.2022.3142859
  20. Bardavelidze, A., Bardavelidze, K. (2024). Development and investigation of algorithm for the synthesis of an automatic control system of the drying process. International Journal on Information Technologies and Security, 16 (1), 15–26. https://doi.org/10.59035/ojbv6115
  21. Chopra, V., Singla, S. K., Dewan, L. (2014). Comparative Analysis of Tuning a PID Controller using Intelligent Methods. Acta Polytechnica Hungarica, 11 (8), 235–249. https://doi.org/10.12700/aph.11.08.2014.08.13
  22. Horbiychuk, M., Lazoriv, N., Chyhur, L., Chyhur, І. (2021). Determining configuration parameters for proportionally integrated differentiating controllers by arranging the poles of the transfer function on the complex plane. Eastern-European Journal of Enterprise Technologies, 5 (2 (113)), 80–93. https://doi.org/10.15587/1729-4061.2021.242869
  23. Ventre, A. G. S. (2023). Determinants and Systems of Linear Equations. Calculus and Linear Algebra. Cham: Springer, 209–241. https://doi.org/10.1007/978-3-031-20549-1_14
  24. Borovska, T. M. (2018). Teorіia avtomatichnogo upravlіnnia. Vіnnitcia: Vіnnitckii natcіonalnii tekhnіchnii unіversitet, 256. Available at: https://pdf.lib.vntu.edu.ua/books/IRVC/2021/Borovska_2018_256.pdf
  25. Newton, Jr., Gould, L. A., Kaiser, J. F. (1957). Analytic design of linear feedback controls. New York, 419.
Розробка комбінованого методу налаштування параметрів ПІ/ПІД-регуляторів для нафтогазових об’єктів

##submission.downloads##

Опубліковано

2025-02-27

Як цитувати

Горбійчук, М. І., Василенчук, М. З., Єднак, І. С., & Лагойда, А. І. (2025). Розробка комбінованого методу налаштування параметрів ПІ/ПІД-регуляторів для нафтогазових об’єктів. Eastern-European Journal of Enterprise Technologies, 1(2 (133), 85–95. https://doi.org/10.15587/1729-4061.2025.322424

Номер

Том 1 № 2 (133) (2025): Інформаційні технології. Системи управління в промисловості

Розділ

Системи управління в промисловості

Ліцензія

Авторське право (c) 2025 Mykhailo Horbiichuk, Mykhailo Vasylenchuk, Ihor Yednak, Andrii Lahoida

Creative Commons License

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.

Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.

Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.