Investigating the stability of oscillations of rectangular plates in an infinitely long rectangular parallelepiped with an ideal fluid
DOI:
https://doi.org/10.15587/1729-4061.2025.323200Keywords:
rectangular plates, ideal fluid, infinitely long rectangular parallelepiped, plane vibrations, stabilityAbstract
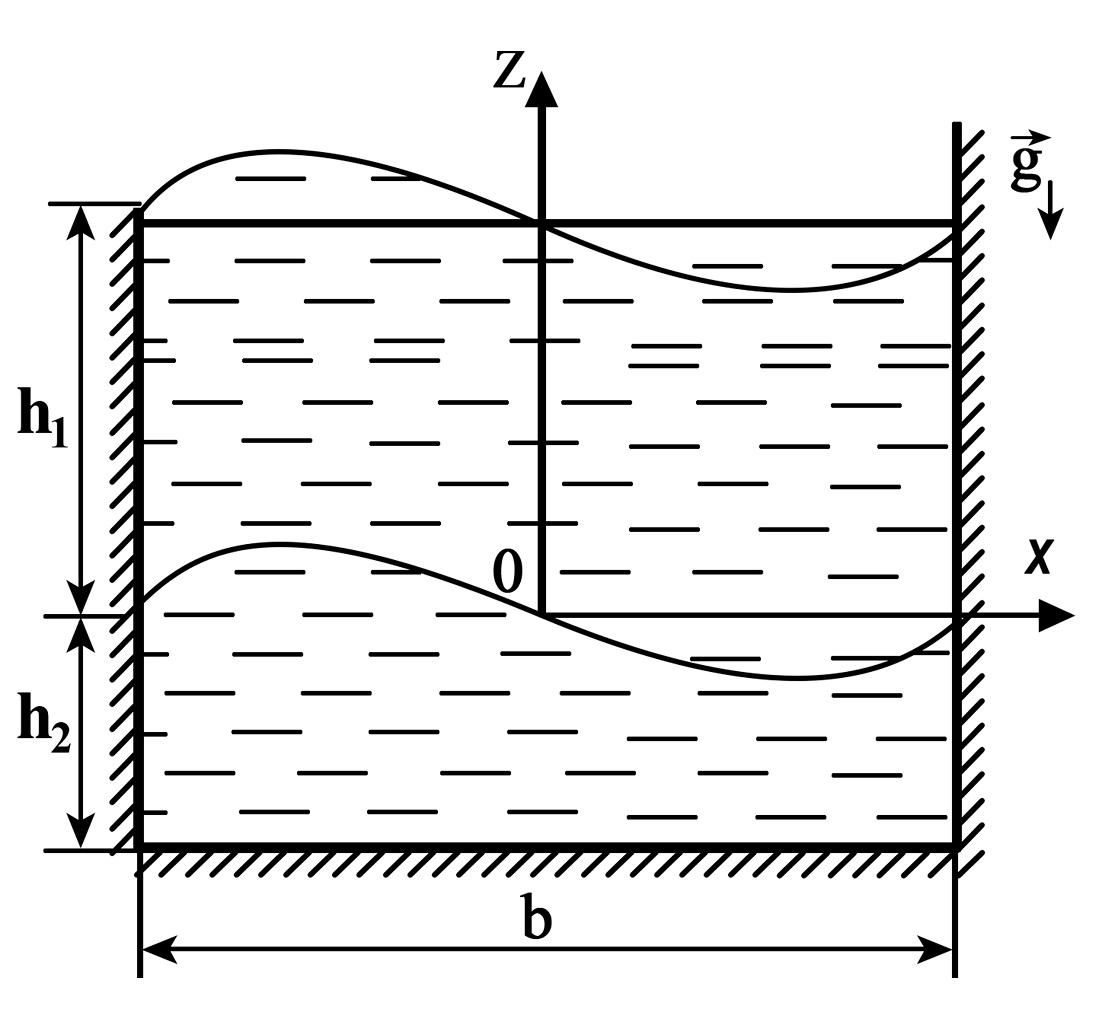
The object of this study is two thin elastic isotropic rectangular plates in an infinitely long rectangular parallelepiped with an ideal fluid. The first plate is the upper base of the rectangular parallelepiped, and the second one horizontally separates ideal fluids that have different densities. The subject of the study is the normal joint plane vibrations of elastic rectangular plates and an incompressible fluid and the conditions that enable the stability of these vibrations.
In the linear statement, the frequency spectrum of normal plane vibrations of two elastic isotropic plates in an infinitely long rectangular parallelepiped with an ideal incompressible fluid has been investigated. The frequency equation of joint vibrations of the plates and the ideal fluid was reduced to the form of an eighth-order determinant for arbitrary cases of fixing the contours of the plates. The case of clamped contours of the plates and the case of rebirth of the plates into membranes is analyzed. Based on analytical studies of infinite series in the transcendental frequency equation, exact stability conditions for the combined oscillations of plates and liquid were established. It has been shown that instability of oscillations of plates and liquid occurs when a heavier liquid is above a less heavy liquid. The derived stability conditions for symmetric and asymmetric oscillations of plates and liquid do not depend on the elastic parameters of the upper plate, the mass characteristics of the plates and the depths of filling liquids. The analytically obtained exact stability conditions for the combined oscillations of the plate and liquid generalize the previously obtained approximate stability conditions for this problem. The numerical calculations of the frequency equation confirmed the analytical studies of the stability conditions. The results could be used in the calculation and design of mechanical objects related to the storage and transportation of liquid cargo
References
- Trocenko, V. A. (1995). Svobodnye kolebaniya zhidkosti v pryamougolnom kanale s uprugoy membranoy na svobodnoy poverhnosti. Prikladnaya mehanika, 31 (8), 74–80.
- Bohun, R. I., Trotsenko, V. A. (2009). Vilni kolyvanni ridyny v priamokutnomu kanali z dovilnym symetrychnym dnom ta pruzhnoiu membranoiu na vilniy poverkhni. Problemy dynamiky ta stiykosti bahatovymirnykh system, 6 (3), 53–76.
- Kononov, Yu. N., Lymar, A. A. (2018). On the update of the conditions of the stability of vibrations of the plate separating ideal liquids in a rectangular channel with hard foundations. Intern. Journal of Mechanical Engineering and Information Technology, 06 (1), 1755–1760.
- Kononov, Y., Lymar, О. (2022). Stability of the coupled liquid-elastic bottom oscillations in a rectangular tank. Journal of Theoretical and Applied Mechanics, Sofia, 52, 164–178. https://doi.org/10.55787/jtams.22.52.2.164
- Jeong, K.-H., Yoo, G.-H., Lee, S.-C. (2004). Hydroelastic vibration of two identical rectangular plates. Journal of Sound and Vibration, 272 (3-5), 539–555. https://doi.org/10.1016/s0022-460x(03)00383-3
- Zhou, D., Liu, W. (2006). Hydroelastic vibrations of flexible rectangular tanks partially filled with liquid. International Journal for Numerical Methods in Engineering, 71 (2), 149–174. https://doi.org/10.1002/nme.1921
- Tariverdilo, S., Shahmardani, M., Mirzapour, J., Shabani, R. (2013). Asymmetric free vibration of circular plate in contact with incompressible fluid. Applied Mathematical Modelling, 37 (1-2), 228–239. https://doi.org/10.1016/j.apm.2012.02.025
- Kononov, Yu. M., Dzhukha, Yu. O. (2020). Vibrations of Two-Layer Ideal Liquid in a Rigid Cylindrical Vessel with Elastic Bases. Journal of Mathematical Sciences, 246 (3), 365–383. https://doi.org/10.1007/s10958-020-04745-w
- Kononov, Yu. M. (2022). Stability of the Equilibrium State of a Rigid Body with Multilayer Ideal Liquid Separated by Elastic Plates. Ukrainian Mathematical Journal, 73 (10), 1551–1565. https://doi.org/10.1007/s11253-022-02013-5
- Kononov, Yu. M. (2023). On the solution of a complicated biharmonic equation in a hydroelasticity problem. Journal of Mathematical Sciences, 274 (3), 340–351. https://doi.org/10.1007/s10958-023-06604-w
- Jeong, K.-H. (2025). Dynamic characteristics of a horizontal rectangular vessel partially or fully filled with a fluid. Nuclear Engineering and Technology, 57 (3), 103258. https://doi.org/10.1016/j.net.2024.10.020
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2025 Yuriy Kononov, Oleksandr Lymar

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.








