Математичний опис згинання поверхні обертання у гвинтовий коноїд

Автор(и)

  • Андрій Вікторович Несвідомін Національний університет біоресурсів і природокористування України, Україна https://orcid.org/0000-0002-9227-4652
  • Сергій Федорович Пилипака Національний університет біоресурсів і природокористування України, Україна https://orcid.org/0000-0002-1496-4615
  • Тетяна Миколаївна Воліна Національний університет біоресурсів і природокористування України, Україна https://orcid.org/0000-0001-8610-2208
  • Михайло Вікторович Каленик Сумський державний педагогічний університет імені А.С. Макаренка, Україна https://orcid.org/0000-0001-7416-4233
  • Світлана Іванівна Ботвіновська Київський національний університет будівництва і архітектури, Україна https://orcid.org/0000-0002-1832-1342
  • Ірина Юріївна Грищенко Національний університет біоресурсів і природокористування України, Україна https://orcid.org/0000-0002-1000-9805
  • Дмитро Васильович Спірінцев Мелітопольський державний педагогічний університет імені Богдана Хмельницького, Україна https://orcid.org/0000-0001-5728-6626
  • Віталій Миколайович Колодненко Сумський національний аграрний університет, Україна https://orcid.org/0000-0002-8450-6759
  • Сергій Петрович Бородай Сумський національний аграрний університет, Україна https://orcid.org/0000-0003-1281-7766
  • Ірина Олександрівна Захарова Сумський державний педагогічний університет імені А. С. Макаренка, Україна https://orcid.org/0000-0002-9693-5550

DOI:

https://doi.org/10.15587/1729-4061.2025.328825

Ключові слова:

крок поверхні, виток шнека, зрізаний конус, наближена розгортка, нерозгортна поверхня

Анотація

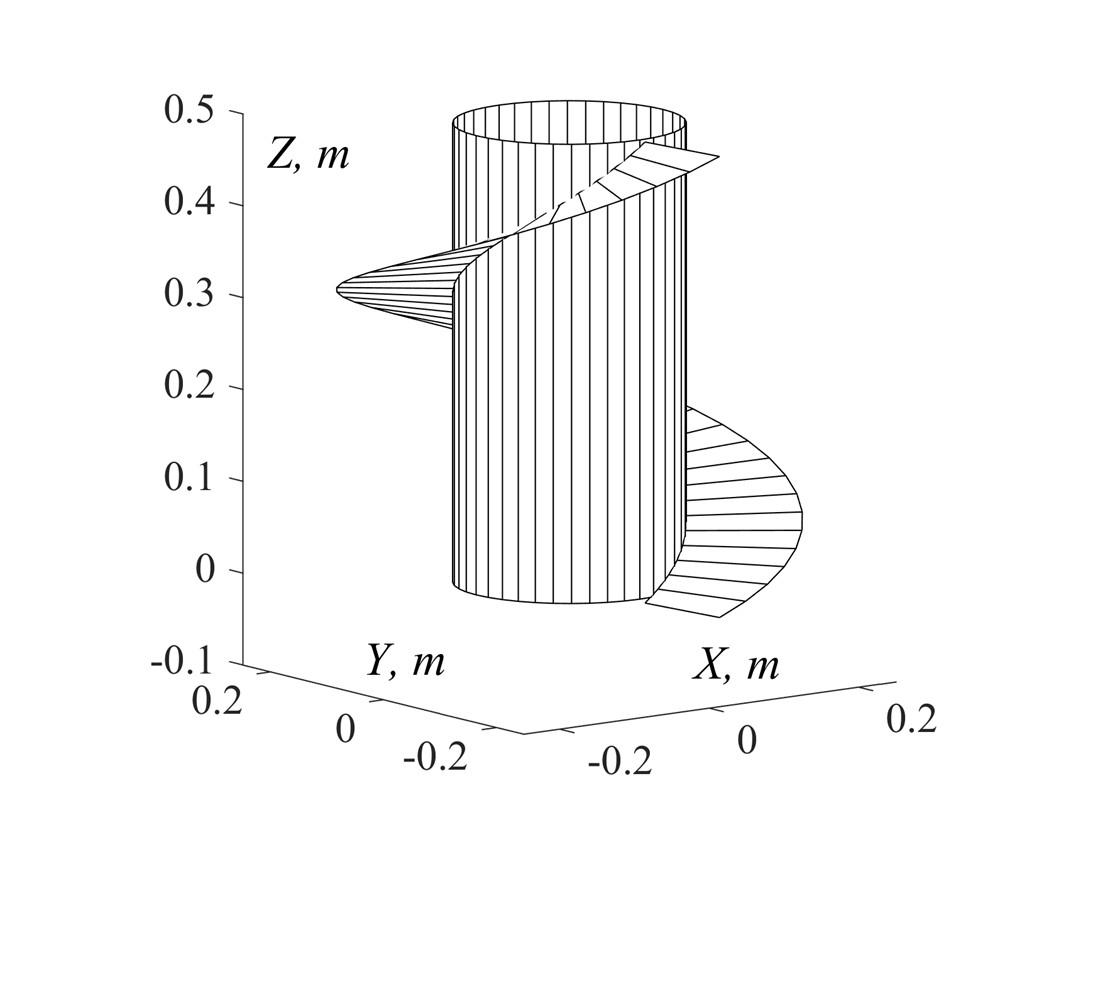
Об’єктом дослідження є процес теоретичного поступового згинання катеноїда у виток гвинтового коноїда. Гвинтовий коноїд або прямий закритий гелікоїд утворюється гвинтовим рухом відрізка навколо осі, причому цей відрізок під час руху перетинає вісь під прямим кутом. Його не можна зігнути на площину, однак поступовим зменшенням кроку можна перетворити у відому поверхню обертання – катеноїд. При такій деформації не змінюються довжини ліній і площа витка в цілому, тобто деформація відбувається подібно до розгортних поверхонь. Така деформація базується на теорії згинань поверхонь окремого розділу диференціальної геометрії. Згідно із нею всяку гвинтову поверхню можна зігнути на поверхню обертання і навпаки. Згинання нерозгортної поверхні гвинтового коноїда на катеноїд є класичним прикладом диференціальної геометрії. Такий підхід дає можливість знайти наближену плоску заготовку для виготовлення витка шнека. Ця проблема вирішується апроксимацією отриманого катеноїда зрізаним конусом. Розгортка зрізаного конуса і буде наближеною розгорткою витка шнека. В цьому полягають особливості знаходження наближеної розгортки, яка в інженерній практиці розраховується за іншими формулами. В цьому також полягає суть отриманих результатів.

В роботі отримано параметричні рівняння, які описують однопараметричну множину проміжних поверхонь при згинанні гвинтового коноїда завдяки поступовому зменшенню кроку поверхні до нуля. В наведеному прикладі розглядається один виток шнека, надітого на вал радіусом r=0,125 м і обмеженого зовнішнім радіусом R=0,25 м при кроці поверхні Н=0,5 м. Розміри зрізаного конуса, який заміняє катеноїда, становлять r=0,148 м для меншої основи, R=0,262 м для більшої основи і Н=0,05 м – для висоти конуса. Вказаних розмірів конуса достатньо, щоб знайти його точну розгортку, яка буде наближеною для витка гвинтового коноїда

Біографії авторів

Андрій Вікторович Несвідомін, Національний університет біоресурсів і природокористування України

Кандидат технічних наук

Кафедра нарисної геометрії, комп’ютерної графіки та дизайну

Сергій Федорович Пилипака, Національний університет біоресурсів і природокористування України

Доктор технічних наук, професор, завідувач кафедри

Кафедра нарисної геометрії, комп’ютерної графіки та дизайну

Тетяна Миколаївна Воліна, Національний університет біоресурсів і природокористування України

Кандидат технічних наук, доцент

Кафедра нарисної геометрії, комп’ютерної графіки та дизайну

Михайло Вікторович Каленик, Сумський державний педагогічний університет імені А.С. Макаренка

Кандидат педагогічних наук, професор, декан

Кафедра математики, фізики та методик їх навчання

Світлана Іванівна Ботвіновська, Київський національний університет будівництва і архітектури

Доктор технічних наук, професор

Кафедра нарисної геометрії та інженерної графіки

Ірина Юріївна Грищенко, Національний університет біоресурсів і природокористування України

Кандидат технічних наук, доцент

Кафедра нарисної геометрії, комп’ютерної графіки та дизайну

Дмитро Васильович Спірінцев, Мелітопольський державний педагогічний університет імені Богдана Хмельницького

Кандидат технічних наук, доцент, завідувач кафедри

Кафедра математики і фізики

Віталій Миколайович Колодненко, Сумський національний аграрний університет

Cтарший викладач

Кафедра транспортних технологій

Сергій Петрович Бородай, Сумський національний аграрний університет

Старший викладач

Кафедра архітектури та інженерних вишукувань

Ірина Олександрівна Захарова, Сумський державний педагогічний університет імені А. С. Макаренка

Кандидат педагогічних наук, доцент

Кафедра менеджменту освіти та педагогіки вищої школи

Посилання

  1. Tian, F., Xia, K., Wang, J., Song, Z., Yan, Y., Li, F., Wang, F. (2021). Design and experiment of self-propelled straw forage crop harvester. Advances in Mechanical Engineering, 13 (7). https://doi.org/10.1177/16878140211024455
  2. Trokhaniak, O. (2022). Estimation of eddy currents and power losses in the rotor of a screw electrothermomechanical converter for additive manufacturing. Machinery & Energetics, 13 (3). https://doi.org/10.31548/machenergy.13(3).2022.92-98
  3. Kresan, Т., Ahmed, A. K., Pylypaka, S., Volina, T., Voloshko, T. (2024). Construction of the working surfaces of the tillage screw body from the compartments of the developable helicoid. Machinery & Energetics, 15 (3), 9–21. https://doi.org/10.31548/machinery/3.2024.09
  4. Klendii, M., Logusch, I., Dragan, A., Tsvartazkii, I., Grabar, A. (2022). Justification and calculation of design and strength parameters of screw loaders. Machinery & Energetics, 13 (4). https://doi.org/10.31548/machenergy.13(4).2022.48-59
  5. He, K., Li, G., Du, Y., Tang, Y. (2019). A digital method for calculation the forming cutter profile in machining helical surface. International Journal of Mechanical Sciences, 155, 370–380. https://doi.org/10.1016/j.ijmecsci.2019.03.018
  6. Rynkovskaya, M. (2018). Support Draft Calculation for a Ramp in the Form of Developable Helicoid. IOP Conference Series: Materials Science and Engineering, 371, 012041. https://doi.org/10.1088/1757-899x/371/1/012041
  7. Lyashuk, O. L., Gypka, A. B., Pundys, Y. I., Gypka, V. V. (2019). Development of design and study of screw working surfaces of auger mechanisms of agricultural machines. Machinery & Energetics, 10 (4), 71–78. Available at: https://technicalscience.com.ua/en/journals/t-10-4-2019/rozrobka-konstruktsiyi-ta-doslidzhyennya-gvintovikh-robochikh-povyerkhon-shnyekovikh-myekhanizmiv-silskogospodarskikh-mashin
  8. Pylypaka, S., Hropost, V., Nesvidomin, V., Volina, T., Kalenyk, M., Volokha, M. et al. (2024). Designing a helical knife for a shredding drum using a sweep surface. Engineering Technological Systems, 4 (1 (130)), 37–44. https://doi.org/10.15587/1729-4061.2024.308195
  9. Junge, S., Zablodskiy, M., Zaiets, N., Chuenko, R., Kovalchuk, S. (2023). The screw-type electrothermomechanical converter as a source of multiphysical influence on the technological environment. Machinery & Energetics, 14 (3), 34–46. https://doi.org/10.31548/machinery/3.2023.34
  10. Mushtruk, M., Gudzenko, M., Palamarchuk, I., Vasyliv, V., Slobodyanyuk, N., Kuts, A. et al. (2020). Mathematical modeling of the oil extrusion process with pre-grinding of raw materials in a twin-screw extruder. Potravinarstvo Slovak Journal of Food Sciences, 14, 937–944. https://doi.org/10.5219/1436
  11. Zablodskiy, M., Kovalchuk, S., Gritsyuk, V., Subramanian, P. (2023). Screw electromechanical hydrolyzer for processing poultry by-products. Machinery & Energetics, 14 (1). https://doi.org/10.31548/machinery/1.2023.36
  12. Romasevych, Y., Loveikin, V., Malinevsky, O. (2022). The method of calculating the maximum torque when jamming the auger of the screw conveyor. Machinery & Energetics, 13 (2). https://doi.org/10.31548/machenergy.13(2).2022.83-90
  13. Trokhaniak, O. (2023). Determination of optimal parameters of hinged operating elements of screw conveyers. Machinery & Energetics, 14 (1). https://doi.org/10.31548/machinery/1.2023.79
  14. Nieszporek, T., Gołębski, R., Boral, P. (2017). Shaping the Helical Surface by the Hobbing Method. Procedia Engineering, 177, 49–56. https://doi.org/10.1016/j.proeng.2017.02.181
  15. Tarelnyk, V. B., Gaponova, O. P., Konoplianchenko, Ye. V., Martsynkovskyy, V. S., Tarelnyk, N. V., Vasylenko, O. O. (2019). Improvement of Quality of the Surface Electroerosive Alloyed Layers by the Combined Coatings and the Surface Plastic Deformation. III. The Influence of the Main Technological Parameters on Microgeometry, Structure and Properties of Electrolytic Erosion Coatings. Metallofizika I Noveishie Tekhnologii, 41 (3), 313–335. https://doi.org/10.15407/mfint.41.03.0313
  16. Tarelnyk, V. B., Gaponova, O. P., Konoplianchenko, Ye. V., Martsynkovskyy, V. S., Tarelnyk, N. V., Vasylenko, O. O. (2019). Improvement of Quality of the Surface Electroerosive Alloyed Layers by the Combined Coatings and the Surface Plastic Deformation. II. The Analysis of a Stressedly-Deformed State of Surface Layer after a Surface Plastic Deformation of Electroerosive Coatings. Metallofizika I Noveishie Tekhnologii, 41 (2), 173–192. https://doi.org/10.15407/mfint.41.02.0173
  17. Chvartatskiy, I., Flonts, I., Grabar, A., Shatrov, R. (2021). Synthesis of energy-saving transport-technological systems with screw working bodies. Machinery & Energetics, 12 (4). https://doi.org/10.31548/machenergy2021.04.077
  18. Gritsyuk, V., Nevliudov, I., Zablodskiy, M., Subramanian, P. (2022). Estimation of eddy currents and power losses in the rotor of a screw electrothermomechanical converter for additive manufacturing. Machinery & Energetics, 13 (2). https://doi.org/10.31548/machenergy.13(2).2022.41-49
  19. Klendiy, M. B., Drahan, A. P. (2021). Substantiation of the design of the working body of the screw section of the combined tillage tool. Perspective technologies and devices, 18, 66–72. https://doi.org/10.36910/6775-2313-5352-2021-18-10
  20. Kresan, T. (2021). Movement of soil particles on surface of developable helicoid with horizontal axis of rotation with given angle of attack. Machinery & Energetics, 12 (2). https://doi.org/10.31548/machenergy2021.02.067
  21. Pylypaka, S., Kresan, Т., Hropost, V., Babka, V., Hryshchenko, I. (2022). Calculation of the bending parameters of a flat workpiece into a twist of a helicoid torso. Machinery & Energetics, 13 (4). https://doi.org/10.31548/machenergy.13(4).2022.81-88
Математичний опис згинання поверхні обертання у гвинтовий коноїд

##submission.downloads##

Опубліковано

2025-06-27

Як цитувати

Несвідомін, А. В., Пилипака, С. Ф., Воліна, Т. М., Каленик, М. В., Ботвіновська, С. І., Грищенко, І. Ю., Спірінцев, Д. В., Колодненко, В. М., Бородай, С. П., & Захарова, І. О. (2025). Математичний опис згинання поверхні обертання у гвинтовий коноїд. Eastern-European Journal of Enterprise Technologies, 3(1 (135), 30–37. https://doi.org/10.15587/1729-4061.2025.328825

Номер

Том 3 № 1 (135) (2025): Виробничо-технологічні системи

Розділ

Виробничо-технологічні системи

Ліцензія

Авторське право (c) 2025 Andrii Nesvidomin, Serhii Pylypaka, Tetiana Volina, Mykhailo Kalenyk, Svitlana Botvinovska, Iryna Hryshchenko, Dmytro Spirintsev, Vitalii Kolodnenko, Serhii Borodai, Irina Zakharova

Creative Commons License

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.

Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.

Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.