Розробка детерміністичного алгоритму на основі варіацій для стохастичних мінімальних кістякових дерев у розподільних мережах

Автор(и)

DOI:

https://doi.org/10.15587/1729-4061.2025.329685

Ключові слова:

кістякове дерево, стохастичний граф, алгоритм на основі дисперсії, детерміністичне перетворення, моделювання невизначеності, оптимізація мережі

Анотація

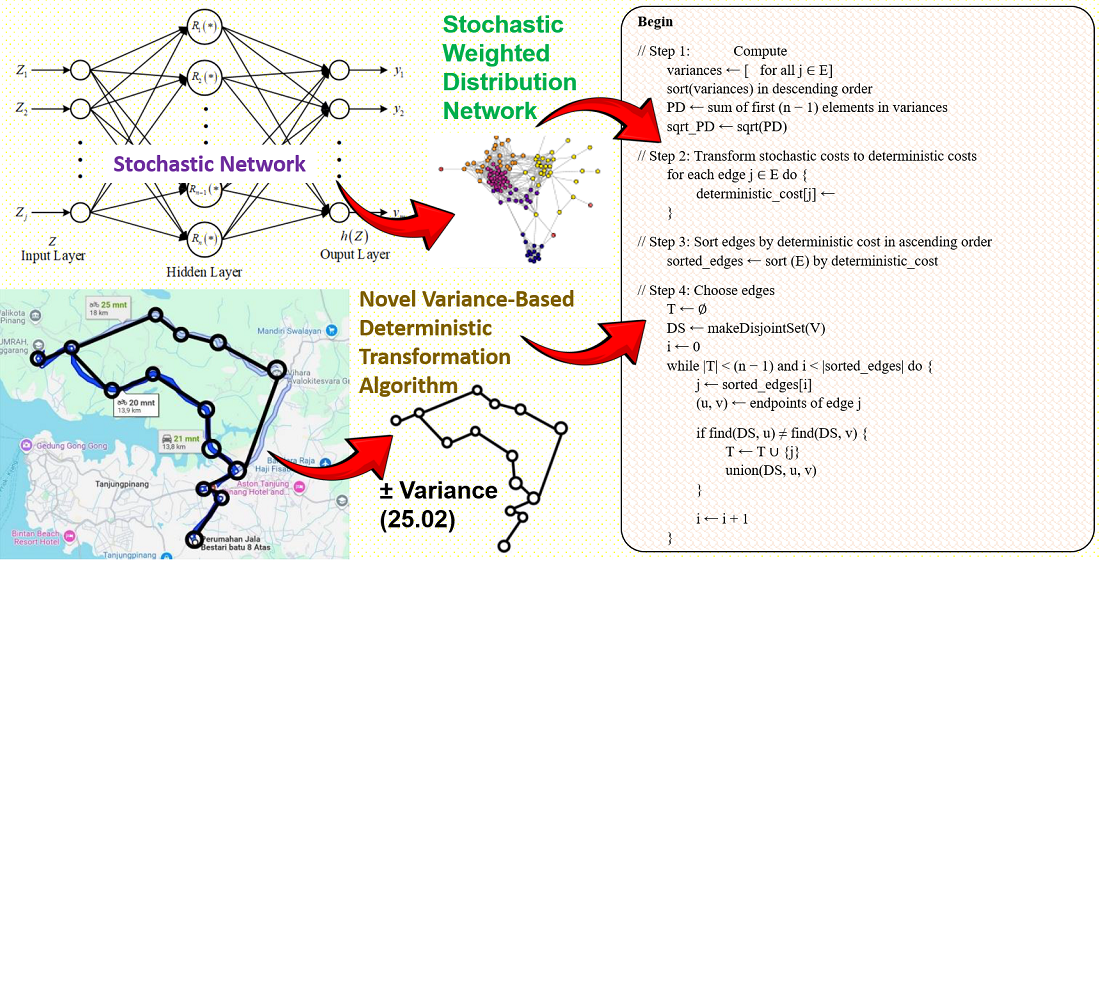
Це дослідження стосується побудови мінімальних кістякових дерев (МКД) у стохастичних зважених розподільних мережах, де витрати на ребра мають невід'ємні невизначеності з відомими середніми значеннями та дисперсіями. Традиційні детерміновані методи часто дають збій, а існуючі стохастичні підходи часто є нестабільними або обчислювально складними за високої невизначеності. Запропоновано новий алгоритм детерміністичного перетворення на основі дисперсії. Його основною особливістю є перетворення стохастичних витрат на ребра в надійні детерміновані еквіваленти шляхом обчислення агрегованого члена дисперсії з найбільших (n – 1) дисперсій ребер, що дозволяє побудувати МКД за допомогою класичних алгоритмів. Цей метод принципово підвищує стабільність і забезпечує доцільність, особливо у сценаріях з високою дисперсією, покращуючи традиційні методи на основі довірчих інтервалів. Ефективність алгоритму була ретельно перевірена. Його продуктивність порівнювали з ймовірнісним методом на основі Qij за помірної дисперсії, демонструючи послідовні та точні МКД. Потім його було застосовано до складної 21-реберної розподільчої мережі з високими параметрами дисперсії. Результати підтверджують широку застосовність, точність та здатність алгоритму будувати надійні кістякові дерева як за помірної, так і за значної невизначеності. Алгоритм демонструє значну обчислювальну ефективність (O(r log r)), що забезпечує практичність та масштабованість при різних рівнях невизначеності. На відміну від ітеративних або моделей з важкими обмеженнями, цей алгоритм спрощує оптимізацію, зберігаючи при цьому представлення невизначеності. Це робить його добре придатним для великомасштабних мереж та реальних систем, де мінливість вартості є критично важливою. Майбутні дослідження включають розширення цього підходу до багатоцільової оптимізації або динамічних мереж

Біографії авторів

Anna Angela Sitinjak, Universitas Sumatera Utara

Magister of Science

Department of Mathematics, Doctoral Program, FMIPA

Saib Suwilo, Universitas Sumatera Utara

Professor, Doctor of Philosophy, Magister of Science

Department of Mathematics, Doctoral Program, FMIPA

Mardiningsih Mardiningsih, Universitas Sumatera Utara

Doctor of Philosophy, Magister of Science

Department of Mathematics, Doctoral Program, FMIPA

Sutarman Sutarman, Universitas Sumatera Utara

Doctor of Philosophy, Magister of Science

Department of Mathematics, Doctoral Program, FMIPA

Посилання

  1. Luo, S., Yimamu, N., Li, Y., Wu, H., Irfan, M., Hao, Y. (2022). Digitalization and sustainable development: How could digital economy development improve green innovation in China? Business Strategy and the Environment, 32 (4), 1847–1871. https://doi.org/10.1002/bse.3223
  2. Feng, R., Qu, X. (2023). Innovation-Driven Industrial Agglomeration Impact on Green Economic Growth in the Yellow River Basin: An Empirical Analysis. Sustainability, 15 (17), 13264. https://doi.org/10.3390/su151713264
  3. Mor, S., Ravindra, K. (2023). Municipal solid waste landfills in lower- and middle-income countries: Environmental impacts, challenges and sustainable management practices. Process Safety and Environmental Protection, 174, 510–530. https://doi.org/10.1016/j.psep.2023.04.014
  4. Sinha, S. K., Davis, C., Gardoni, P., Babbar-Sebens, M., Stuhr, M., Huston, D. et al. (2023). Water Sector Infrastructure Systems Resilience A Social-Ecological-Technical System-of-Systems and Whole-Life Approach. Cambridge Prisms: Water, 1–50. https://doi.org/10.1017/wat.2023.3
  5. Israilova, E., Voronina, A., Shatila, K. (2023). Impact of water scarcity on socio-economic development. E3S Web of Conferences, 458, 08027. https://doi.org/10.1051/e3sconf/202345808027
  6. Koutsokosta, A., Katsavounis, S. (2024). Stochastic transitions of a mixed-integer linear programming model for the construction supply chain: chance-constrained programming and two-stage programming. Operational Research, 24 (3). https://doi.org/10.1007/s12351-024-00856-3
  7. Talebi, A., Haeri Boroujeni, S. P., Razi, A. (2024). Integrating random regret minimization-based discrete choice models with mixed integer linear programming for revenue optimization. Iran Journal of Computer Science, 8 (1), 21–35. https://doi.org/10.1007/s42044-024-00193-w
  8. Heidari, A., Shishehlou, H., Darbandi, M., Navimipour, N. J., Yalcin, S. (2024). A reliable method for data aggregation on the industrial internet of things using a hybrid optimization algorithm and density correlation degree. Cluster Computing, 27 (6), 7521–7539. https://doi.org/10.1007/s10586-024-04351-4
  9. Ishii, H., Shiode, S., Nishida, T., Namasuya, Y. (1981). Stochastic spanning tree problem. Discrete Applied Mathematics, 3 (4), 263–273. https://doi.org/10.1016/0166-218x(81)90004-4
  10. Akbari Torkestani, J., Meybodi, M. R. (2010). A learning automata-based heuristic algorithm for solving the minimum spanning tree problem in stochastic graphs. The Journal of Supercomputing, 59 (2), 1035–1054. https://doi.org/10.1007/s11227-010-0484-1
  11. Zhao, L., Huang, Y., Dai, Q., Yang, L., Chen, F., Wang, L. et al. (2019). Multistage Active Distribution Network Planning With Restricted Operation Scenario Selection. IEEE Access, 7, 121067–121080. https://doi.org/10.1109/access.2019.2936936
  12. Xu, Y., Zhang, L. (2023). Target-based Distributionally Robust Minimum Spanning Tree Problem. arXiv. https://doi.org/10.48550/arXiv.2311.10670
  13. Hoeksma, R., Speek, G., Uetz, M. (2024). Stochastic Minimum Spanning Trees with a Single Sample. arXiv. https://doi.org/10.48550/arXiv.2409.16119
  14. Mathwieser, C., Çela, E. (2024). Special cases of the minimum spanning tree problem under explorable edge and vertex uncertainty. Networks, 83 (3), 587–604. https://doi.org/10.1002/net.22204
  15. Makowiec, L., Salvi, M., Sun, R. (2024). Random spanning trees in random environment. arXiv. https://doi.org/10.48550/arXiv.2410.16830
  16. Adhikary, K., Pal, P., Poray, J. (2024). The minimum spanning tree problem on networks with neutrosophic numbers. Neutrosophic Sets and Systems, 63, 258–270. Available at: https://fs.unm.edu/NSS/SpanningTree16.pdf
  17. Hu, Z., Sun, W., Zhu, S. (2022). Chance constrained programs with Gaussian mixture models. IISE Transactions, 54 (12), 1117–1130. https://doi.org/10.1080/24725854.2021.2001608
  18. Chatterjee, S., Pandurangan, G., Pham, N. D. (2020). Distributed MST. Proceedings of the 21st International Conference on Distributed Computing and Networking, 1–10. https://doi.org/10.1145/3369740.3369778
Розробка детерміністичного алгоритму на основі варіацій для стохастичних мінімальних кістякових дерев у розподільних мережах

##submission.downloads##

Опубліковано

2025-06-25

Як цитувати

Sitinjak, A. A., Suwilo, S., Mardiningsih, M., & Sutarman, S. (2025). Розробка детерміністичного алгоритму на основі варіацій для стохастичних мінімальних кістякових дерев у розподільних мережах. Eastern-European Journal of Enterprise Technologies, 3(4 (135), 42–51. https://doi.org/10.15587/1729-4061.2025.329685

Номер

Том 3 № 4 (135) (2025): Математика та кібернетика - прикладні аспекти

Розділ

Математика та кібернетика - прикладні аспекти

Ліцензія

Авторське право (c) 2025 Anna Angela Sitinjak, Saib Suwilo, Mardiningsih Mardiningsih, Sutarman Sutarman

Creative Commons License

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.

Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.

Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.