Аналітичний опис у точковій формі способу графічного диференціювання плоскої кривої лінії
DOI:
https://doi.org/10.15587/1729-4061.2025.343387Ключові слова:
точковий поліном, смуга дифпроєкцій, апроксимація, аналітизація методу хорд, аналітизація креслениківАнотація
Об’єктом дослідження є графічне диференціювання, зокрема – метод хорд, як один із варіантів графічного диференціювання щодо заміни графічних операцій на аналітичні у точковій формі.
Визначення точки відліку і центру проєктування для побудови смуги дифпроєкції корелюють її положення щодо значень похідної функції, яка графічно подається дискретним рядом точок. Точка відліку, права дифпроєкція першої та ліва дифпроєкція другої точок мають однакові значення у полі похідних. Однак вони не збігаються зі значеннями похідних вихідних функцій. Для встановлення такої відповідності різницю між лівою і правою дифпроєкціями першої точки ділять навпіл та віднімають від першої похідної вихідної функції – точкового поліному.
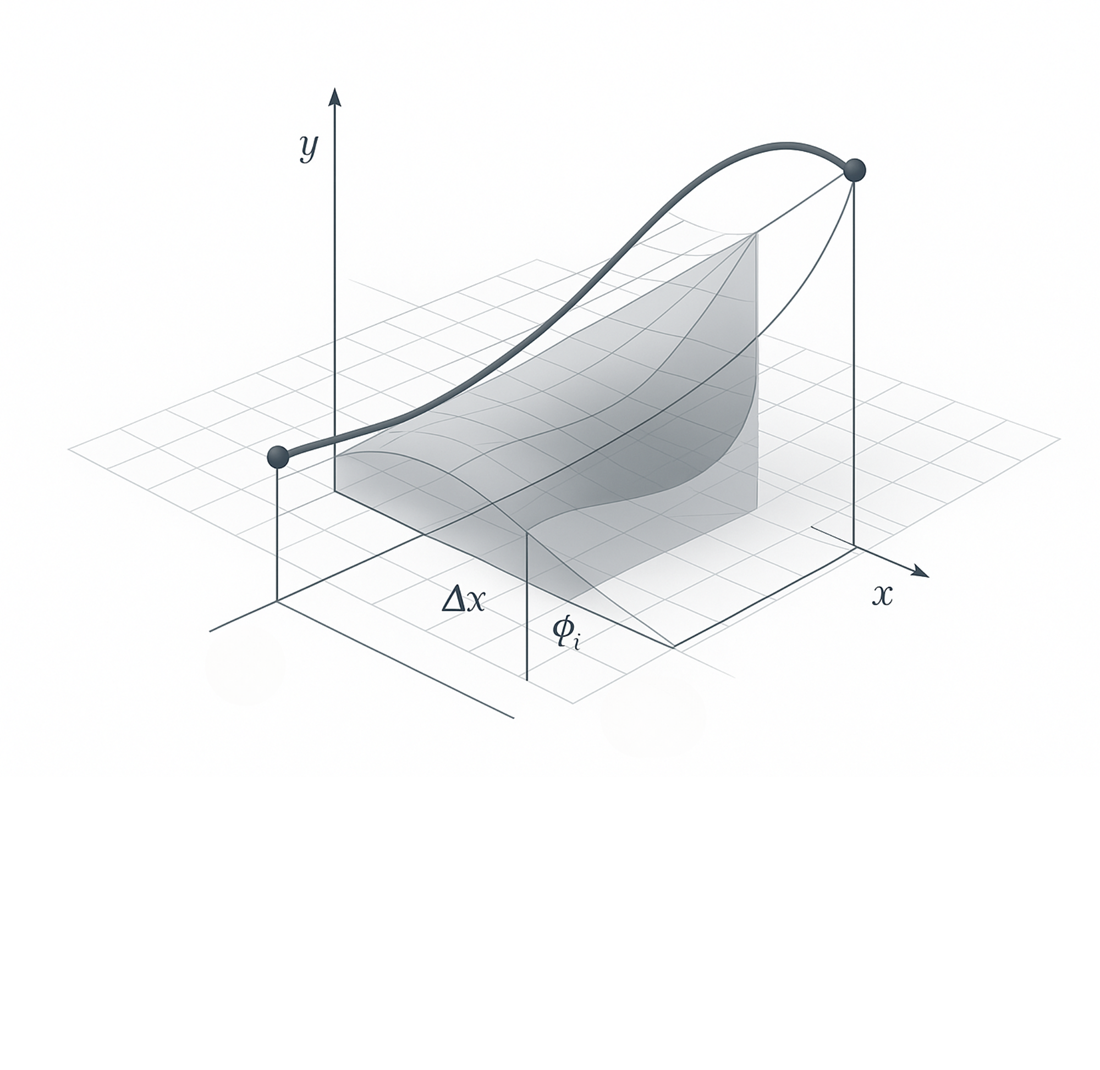
Відносно точки відліку, паралельно першій ланці супровідної ламаної лінії дискретно поданої кривої проводиться пряма, що перетинає вісь абсцис в центрі проєктування. Знаходження точки відліку та центру проєктування здійснюється аналітично у точковій формі без будь-яких графічних операцій. Із центру проєктування проводяться промені, паралельні одній із ланок супровідної ламаної лінії, утворюючи таким чином смугу дифпроєкцій, всередині якої обираються значення кутів нахилів дотичних до кривої в базисних точках. Дискретні значення похідних з’єднуються відтинками прямих або залишаються окремими точками. Отримані значення похідних збігаються з аналітичними значеннями з відхиленням не більше 0,5–1,5 одиниць. Розроблені алгоритми можуть бути інтегровані в системи автоматизованого проєктування та інженерного аналізу для ефективного обчислення похідних дискретно заданих кривих. Крім того, вони можуть слугувати основою для створення обчислювально-продуктивних модулів у системах штучного інтелекту та цифрової обробки даних, що працюють з геометричними та дискретними масивами інформації
Посилання
- Fischer, M., Krause, C. M. (2025). Pivotal examples in graphical differentiation – an analysis of semiotic and theoretic control. Proceedings of the 48th Conference of the International Group for the Psychology of Mathematics Education: Research Reports, 1, 259–266. Available at: https://www.researchgate.net/publication/392626925_PIVOTAL_EXAMPLES_IN_GRAPHICAL_DIFFERENTIATION_-AN_ANALYSIS_OF_SEMIOTIC_AND_THEORETIC_CONTROL
- Zakharova, I., Shchetynin, S., Shchetynina, V., Zusin, A., Volenko, I. (2025). Use of robotic and automated systems in welding and restoration of parts. Machinery & Energetics, 16 (1), 117–129. https://doi.org/10.31548/machinery/1.2025.117
- Aghayeva, K., Krauklit, G. (2025). Automated methane emission monitoring systems based on satellite data: Radiation transfer model analysis. Machinery & Energetics, 16 (1), 146–156. https://doi.org/10.31548/machinery/1.2025.146
- Turchyn, O. (2024). Introduction of neural network technologies to optimise the control of the operating modes of a sucker-rod pump installation. Machinery & Energetics, 16 (1), 32–42. https://doi.org/10.31548/machinery/1.2025.32
- Andriievskyi, I., Spivak, S., Gogota, O., Yermolenko, R. (2024). Application of the regression neural network for the analysis of the results of ultrasonic testing. Machinery & Energetics, 15 (1), 43–55. https://doi.org/10.31548/machinery/1.2024.43
- Mukherjee, S., Claassen, M., Bürkner, P.-C. (2025). DGP-LVM: Derivative Gaussian process latent variable models. Statistics and Computing, 35 (5). https://doi.org/10.1007/s11222-025-10644-4
- Shahan, J. T., Walker, S. W. (2025). Exact shape derivatives with unfitted finite element methods. Journal of Numerical Mathematics. https://doi.org/10.1515/jnma-2024-0113
- Guo, P., Lan, Y., Qiao, J. (2025). Exact solutions of differential equations: renormalization group based polynomial scheme. Communications in Theoretical Physics, 77 (10), 105005. https://doi.org/10.1088/1572-9494/add24e
- Konopatskiy, E. V., Bezditnyi, A. A. (2019). Geometric modeling and optimization of multidimensional data in Radischev integrated drawing. Journal of Physics: Conference Series, 1260 (7), 072006. https://doi.org/10.1088/1742-6596/1260/7/072006
- Konopatskiy, E. V., Mashtaler, S. N., Bezditnyi, A. A. (2019). Study of high-strength steel fiber concrete strength characteristics under elevated temperatures using mathematical modelling methods. IOP Conference Series: Materials Science and Engineering, 687 (2), 022040. https://doi.org/10.1088/1757-899x/687/2/022040
- Konopatskiy, E. V., Bezditnyi, A. A. (2020). Geometric modeling of multifactor processes and phenomena by the multidimensional parabolic interpolation method. Journal of Physics: Conference Series, 1441 (1), 012063. https://doi.org/10.1088/1742-6596/1441/1/012063
- Lako, A., Barko, O. (2024). Design and optimisation of automated hydraulic gate control systems for flood control. Machinery & Energetics, 15 (4), 58–68. https://doi.org/10.31548/machinery/4.2024.58
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2025 Viktor Vereschaga, Kseniia Lysenko, Yevhen Adoniev, Ernest Murtaziiev, Ivan Vereshchaha, Tetiana Volina

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.
Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.










