Determining the patterns of asymmetric interaction of plastic medium with counter-directional metal flow

Authors

DOI:

https://doi.org/10.15587/1729-4061.2024.293842

Keywords:

loading asymmetry, counter-directional metal flow, plane problem, effects of plastic deformation

Abstract

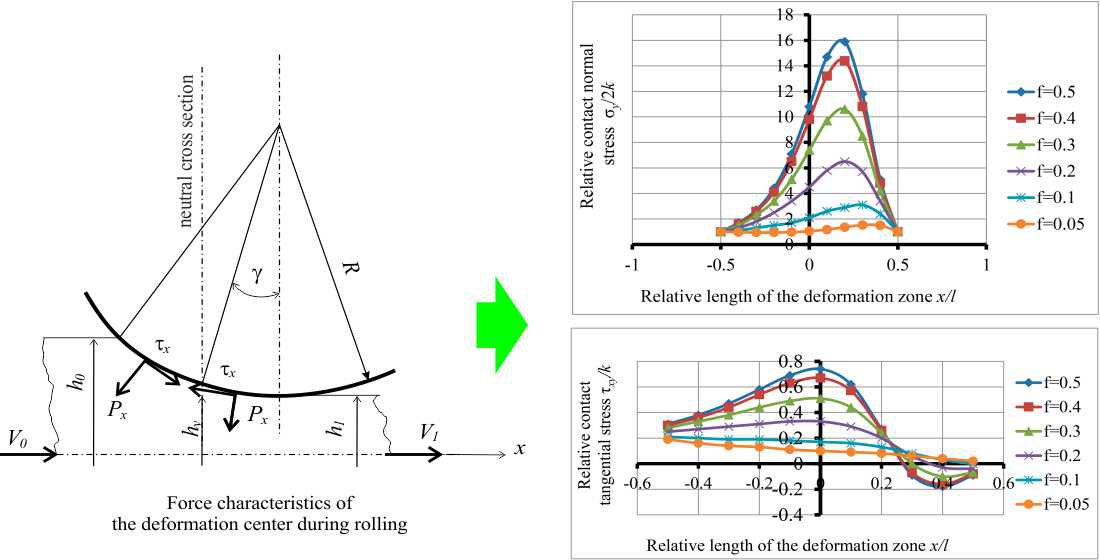
The plane problem of rolling theory is analytically solved using the method argument of functions of a complex variable. The solution to the plane problem has been strengthened from the point of view of the asymmetry of the process, which made it possible to consider the applied problem as the interaction of differently directed zones in the deformation zone. The interaction of lagging and advancing zones is represented as a combination of multidirectional processes in a single deformation zone. With a change in kinematic, power characteristics in local zones, the process parameters change in the entire deformation zone. Stressed states of intermediate loading schemes between stable and unstable rolling are considered. A feature of the interaction of zones with the opposite flow of metal is the analogy with the action of back tension on the deformation zone in literally all parameters - this is the presence of tensile stresses in the lagging zone, a decrease in local specific pressures, a shift in maximum normal stresses towards the exit from the rolls, a change in the length of the advance zone, reduction in rolling force.

The studies confirm and repeat the generally accepted provisions of the theory of rolling but reveal the effects of changes in the stress state under different loading models.

The results of the work make it possible to determine the modes of rolling processes visually and computationally under conditions of strong and weak interaction of zones with an oppositely directed metal flow.

The effects of plastic deformation with a decrease in the total effort in the processes that are within the reach of the limiting focus of crimping under conditions of increasing kinematic load when the gripping angles vary between 0,077…0,168 are given

Author Biographies

Valeriy Chigirinsky, Rudny Industrial Institute

Doctor of Technical Sciences, Professor

Department of Metallurgy and Mining

Abdrakhman Naizabekov, Rudny Industrial Institute

Doctor of Technical Sciences, Professor, Chairman of the Management Board-Rector

Department of Metallurgy and Mining

Sergey Lezhnev, Rudny Industrial Institute

PhD, Associate Professor

Department of Metallurgy and Mining

Olena Naumenko, Dnipro University of Technology

Senior Lecturer

Department of Mechanical and Biomedical Engineering

Sergey Kuzmin, Rudny Industrial Institute

PhD

Department of Metallurgy and Mining

References

  1. Maksymenko, O. P., Loboiko, D. Y., Shtoda, M. N., Shtoda, Y. Y. (2018). Issledovanie prodolnoi ustoichivosti polosy pri prokatke na nepreryvnykh stanakh. Zbirnyk naukovykh prats Dniprovskoho derzhavnoho tekhnichnoho universytetu. Tekhnichni nauky. Tem. vyp., 59–64.
  2. Maksimenko, O. P., Romaniuk, R. Ia. (2009). Analiz prodolnoi ustoichivosti protcessa prokatki s uchetom vnutrennikh sil i rezhima natiazheniia polosy. Izvestiia vuzov. Chernaia metallurgiia, 10, 32–34.
  3. Grudev, A. P. (1998). Zakhvatyvaiushchaia sposobnost prokatnykh valkov. Moscow: SP Intermet Inzhiniring, 283.
  4. Ryabov, P. N. (2017). The features of plastic flow localization in materials under shear deformations. AIP Conference Proceedings. doi: https://doi.org/10.1063/1.4992562
  5. Vabishchevich, M., Zatyliuk, G. (2021). Analysis of the stressed-strained state of the foundation-shell at interaction with the elastic-plastic medium. Strength of Materials and Theory of Structures, 106, 105–112. doi: https://doi.org/10.32347/2410-2547.2021.106.105-112
  6. Solodei, I., Petrenko, E., Zatyliuk, G. (2020). Nonlinear problem of structural deformation in interaction with elastoplastic medium. Strength of Materials and Theory of Structures, 105, 48–63. doi: https://doi.org/10.32347/2410-2547.2020.105.48-63
  7. Rogov, Ye. I., Kussainov, A. A., Gumenyuk, V. V. (2018). Physical models of solid mass and related processes in interaction with foundations. Journal of Mechanical Engineering Research & Developments, 41 (2), 65–74. doi: https://doi.org/10.26480/jmerd.02.2018.65.74
  8. Vasidzu, K. (1987). Variatcionnye metody v teorii uprugosti i plastichnosti. Moscow: Mir, 542.
  9. Kolmogorov, V. L. (1986). Mekhanika obrabotki metallov davleniem. Moscow: Metallurgiia, 686.
  10. Gun, G. Ia. (1980). Teoreticheskie osnovy obrabotki metallov davleniem. Moscow: Metallurgiia, 456.
  11. Tarnovskii, I. Ia., Pozdeev, A. A., Ganago, O. A. et al. (1963). Teoriia obrabotki metallov davleniem. Moscow: Metallurgizdat, 673.
  12. Zubchaninov, V. G. (2002). Matematicheskaia teoriia plastichnosti. Tver: TGTU, 300.
  13. Krysko, A. V., Papkova, I. V., Rezchikov, A. F., Krysko, V. A. (2022). A New Mathematical Model of Functionally Graded Porous Euler–Bernoulli Nanoscaled Beams Taking into Account Some Types of Nonlinearities. Materials, 15 (20), 7186. doi: https://doi.org/10.3390/ma15207186
  14. Bondar, V. S., Danshin, V. V. (2008). Plastichnost. Proportcionalnye i neproportcionalnye nagruzheniia. Moscow: Fizmatlit, 176.
  15. Chigirinsky, V., Naizabekov, A., Lezhnev, S. (2021). Сlosed problem of plasticity theory. Journal of Chemical Technology and Metallurgy, 56 (4), 867–876.
  16. Timoshenko, S. P., Guder, Dzh. (1979). Teoriia uprugosti. Moscow: Nauka, 560.
  17. Dorofeyev, O. A., Kovtun, V. V. (2019). Estimation of the Stress-Strain State of a Discrete Medium by a Plastic Flow Model. Problems of tribology, 93 (3), 29–38. doi: https://doi.org/10.31891/2079-1372-2019-93-3-29-38
  18. Andersen, R. G., Londono, J. G., Woelke, P. B., Nielsen, K. L. (2020). Fundamental differences between plane strain bending and far-field plane strain tension in ductile plate failure. Journal of the Mechanics and Physics of Solids, 141. doi: https://doi.org/10.1016/j.jmps.2020.103960
  19. Stampouloglou, I. H., Theotokoglou, E. E. (2009). Additional Separated-Variable Solutions of the Biharmonic Equation in Polar Coordinates. Journal of Applied Mechanics, 77 (2). doi: https://doi.org/10.1115/1.3197157
  20. El-Naaman, S. A., Nielsen, K. L., Niordson, C. F. (2019). An investigation of back stress formulations under cyclic loading. Mechanics of Materials, 130, 76–87. doi: https://doi.org/10.1016/j.mechmat.2019.01.005
  21. Lopez-Crespo, P., Camas, D., Antunes, F. V., Yates, J. R. (2018). A study of the evolution of crack tip plasticity along a crack front. Theoretical and Applied Fracture Mechanics, 98, 59–66. doi: https://doi.org/10.1016/j.tafmec.2018.09.012
  22. Li, J., Zhang, Z., Li, C. (2017). Elastic-plastic stress-strain calculation at notch root under monotonic, uniaxial and multiaxial loadings. Theoretical and Applied Fracture Mechanics, 92, 33–46. doi: https://doi.org/10.1016/j.tafmec.2017.05.005
  23. Pathak, H. (2017). Three-dimensional quasi-static fatigue crack growth analysis in functionally graded materials (FGMs) using coupled FE-XEFG approach. Theoretical and Applied Fracture Mechanics, 92, 59–75. doi: https://doi.org/10.1016/j.tafmec.2017.05.010
  24. Correia, J. A. F. O., Huffman, P. J., De Jesus, A. M. P., Cicero, S., Fernández-Canteli, A., Berto, F., Glinka, G. (2017). Unified two-stage fatigue methodology based on a probabilistic damage model applied to structural details. Theoretical and Applied Fracture Mechanics, 92, 252–265. doi: https://doi.org/10.1016/j.tafmec.2017.09.004
  25. Kovalevska, I., Samusia, V., Kolosov, D., Snihur, V., Pysmenkova, T. (2020). Stability of the overworked slightly metamorphosed massif around mine working. Mining of Mineral Deposits, 14 (2), 43–52. doi: https://doi.org/10.33271/mining14.02.043
  26. Sinekop, N. S., Lobanova, L. S., Parkhomenko, L. A. (2015). Metod R–funktcii v dinamicheskikh zadachakh teorii uprugosti. Kharkiv: KhGUPT, 95.
  27. Hussein, N. S. (2014). Solution of a Problem Linear Plane Elasticity with Mixed Boundary Conditions by the Method of Boundary Integrals. Mathematical Problems in Engineering, 2014, 1–11. doi: https://doi.org/10.1155/2014/323178
  28. Chigirinsky, V., Putnoki, A. (2017). Development of a dynamic model of transients in mechanical systems using argument-functions. Eastern-European Journal of Enterprise Technologies, 3 (7 (87)), 11–22. doi: https://doi.org/10.15587/1729-4061.2017.101282
  29. Chigirinsky, V., Naumenko, O. (2019). Studying the stressed state of elastic medium using the argument functions of a complex variable. Eastern-European Journal of Enterprise Technologies, 5 (7 (101)), 27–35. doi: https://doi.org/10.15587/1729-4061.2019.177514
  30. Chigirinsky, V., Naumenko, O. (2020). Invariant differential generalizations in problems of the elasticity theory as applied to polar coordinates. Eastern-European Journal of Enterprise Technologies, 5 (7 (107)), 56–73. doi: https://doi.org/10.15587/1729-4061.2020.213476
  31. Chigirinsky, V., Naumenko, O. (2021). Advancing a generalized method for solving problems of continuum mechanics as applied to the Cartesian coordinate system. Eastern-European Journal of Enterprise Technologies, 5 (7 (113)), 14–24. doi: https://doi.org/10.15587/1729-4061.2021.241287
  32. Tcelikov, A. I. (1962). Teoriia rascheta usilii v prokatnykh stanakh. Moscow: Metallurgizdat, 494.
  33. Arkulis, G. E., Dorogobid, V. G. (1987). Teoriia plastichnosti. Moscow: Metallurgiia, 251.
  34. Tikhonov, A. N., Samarskii, A. A. (1999). Uravneniia matematicheskoi fiziki. Moscow: Izd-vo MGU, 799.
  35. Muskhelishvili, N. I. (1966). Nekotorye osnovnye zadachi matematicheskoi teorii uprugosti. Moscow: Nauka, 709.
  36. Kolmogorov, V. L. (1970). Napriazheniia, deformatcii, razrusheniia. Moscow: Metallurgiia, 230.
  37. Klimenko, P. L. (2007). Kontaktnye napriazheniia pri prokatke. Dnepropetrovsk: POROGI, 285.
  38. Pozdeev, A. A., Tarnovskii, V. I. (1959). O raschete konechnykh peremeshchenii po ikh prirashcheniiam pri OMD. Izvestiia vuzov. Chernaia metallurgiia, 6, 43–52.
  39. Chigirinsky, V., Naizabekov, A., Lezhnev, S., Kuzmin, S., Naumenko, O. (2022). Solving applied problems of elasticity theory in geomechanics using the method of argument functions of a complex variable. Eastern-European Journal of Enterprise Technologies, 5 (7 (119)), 105–113. doi: https://doi.org/10.15587/1729-4061.2022.265673
Determining the patterns of asymmetric interaction of plastic medium with counter-directional metal flow

Downloads

Published

2024-02-28

How to Cite

Chigirinsky, V., Naizabekov, A., Lezhnev, S., Naumenko, O., & Kuzmin, S. (2024). Determining the patterns of asymmetric interaction of plastic medium with counter-directional metal flow. Eastern-European Journal of Enterprise Technologies, 1(7 (127), 66–82. https://doi.org/10.15587/1729-4061.2024.293842

Issue

Vol. 1 No. 7 (127) (2024): Applied mechanics

Section

Applied mechanics

License

Copyright (c) 2023 Valeriy Chigirinsky, Abdrakhman Naizabekov, Sergey Lezhnev, Olena Naumenko, Sergey Kuzmin

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.