Determining the patterns of asymmetric interaction of plastic medium with counter-directional metal flow
DOI:
https://doi.org/10.15587/1729-4061.2024.293842Keywords:
loading asymmetry, counter-directional metal flow, plane problem, effects of plastic deformationAbstract
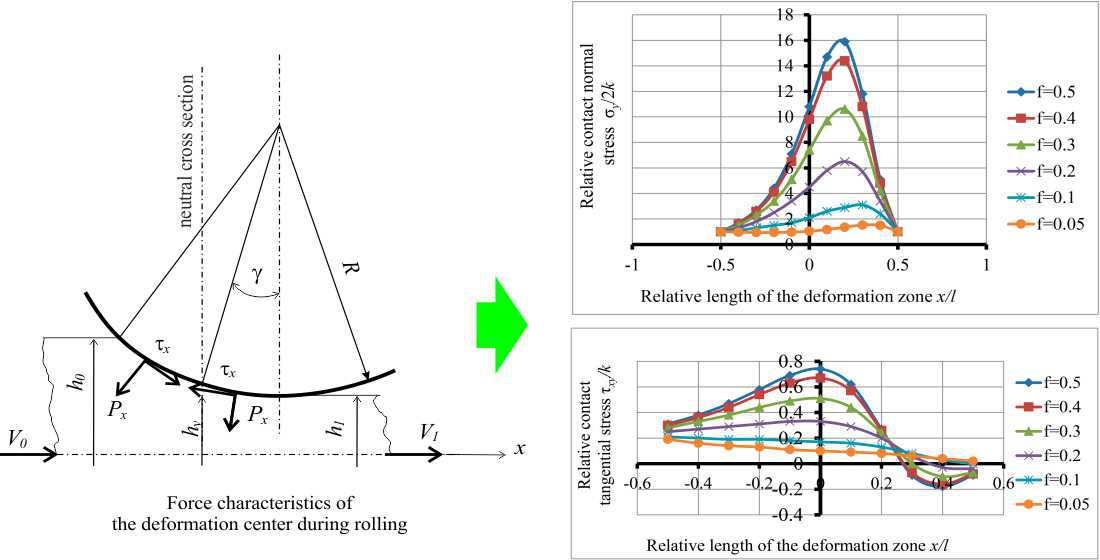
The plane problem of rolling theory is analytically solved using the method argument of functions of a complex variable. The solution to the plane problem has been strengthened from the point of view of the asymmetry of the process, which made it possible to consider the applied problem as the interaction of differently directed zones in the deformation zone. The interaction of lagging and advancing zones is represented as a combination of multidirectional processes in a single deformation zone. With a change in kinematic, power characteristics in local zones, the process parameters change in the entire deformation zone. Stressed states of intermediate loading schemes between stable and unstable rolling are considered. A feature of the interaction of zones with the opposite flow of metal is the analogy with the action of back tension on the deformation zone in literally all parameters - this is the presence of tensile stresses in the lagging zone, a decrease in local specific pressures, a shift in maximum normal stresses towards the exit from the rolls, a change in the length of the advance zone, reduction in rolling force.
The studies confirm and repeat the generally accepted provisions of the theory of rolling but reveal the effects of changes in the stress state under different loading models.
The results of the work make it possible to determine the modes of rolling processes visually and computationally under conditions of strong and weak interaction of zones with an oppositely directed metal flow.
The effects of plastic deformation with a decrease in the total effort in the processes that are within the reach of the limiting focus of crimping under conditions of increasing kinematic load when the gripping angles vary between 0,077…0,168 are given
References
- Maksymenko, O. P., Loboiko, D. Y., Shtoda, M. N., Shtoda, Y. Y. (2018). Issledovanie prodolnoi ustoichivosti polosy pri prokatke na nepreryvnykh stanakh. Zbirnyk naukovykh prats Dniprovskoho derzhavnoho tekhnichnoho universytetu. Tekhnichni nauky. Tem. vyp., 59–64.
- Maksimenko, O. P., Romaniuk, R. Ia. (2009). Analiz prodolnoi ustoichivosti protcessa prokatki s uchetom vnutrennikh sil i rezhima natiazheniia polosy. Izvestiia vuzov. Chernaia metallurgiia, 10, 32–34.
- Grudev, A. P. (1998). Zakhvatyvaiushchaia sposobnost prokatnykh valkov. Moscow: SP Intermet Inzhiniring, 283.
- Ryabov, P. N. (2017). The features of plastic flow localization in materials under shear deformations. AIP Conference Proceedings. doi: https://doi.org/10.1063/1.4992562
- Vabishchevich, M., Zatyliuk, G. (2021). Analysis of the stressed-strained state of the foundation-shell at interaction with the elastic-plastic medium. Strength of Materials and Theory of Structures, 106, 105–112. doi: https://doi.org/10.32347/2410-2547.2021.106.105-112
- Solodei, I., Petrenko, E., Zatyliuk, G. (2020). Nonlinear problem of structural deformation in interaction with elastoplastic medium. Strength of Materials and Theory of Structures, 105, 48–63. doi: https://doi.org/10.32347/2410-2547.2020.105.48-63
- Rogov, Ye. I., Kussainov, A. A., Gumenyuk, V. V. (2018). Physical models of solid mass and related processes in interaction with foundations. Journal of Mechanical Engineering Research & Developments, 41 (2), 65–74. doi: https://doi.org/10.26480/jmerd.02.2018.65.74
- Vasidzu, K. (1987). Variatcionnye metody v teorii uprugosti i plastichnosti. Moscow: Mir, 542.
- Kolmogorov, V. L. (1986). Mekhanika obrabotki metallov davleniem. Moscow: Metallurgiia, 686.
- Gun, G. Ia. (1980). Teoreticheskie osnovy obrabotki metallov davleniem. Moscow: Metallurgiia, 456.
- Tarnovskii, I. Ia., Pozdeev, A. A., Ganago, O. A. et al. (1963). Teoriia obrabotki metallov davleniem. Moscow: Metallurgizdat, 673.
- Zubchaninov, V. G. (2002). Matematicheskaia teoriia plastichnosti. Tver: TGTU, 300.
- Krysko, A. V., Papkova, I. V., Rezchikov, A. F., Krysko, V. A. (2022). A New Mathematical Model of Functionally Graded Porous Euler–Bernoulli Nanoscaled Beams Taking into Account Some Types of Nonlinearities. Materials, 15 (20), 7186. doi: https://doi.org/10.3390/ma15207186
- Bondar, V. S., Danshin, V. V. (2008). Plastichnost. Proportcionalnye i neproportcionalnye nagruzheniia. Moscow: Fizmatlit, 176.
- Chigirinsky, V., Naizabekov, A., Lezhnev, S. (2021). Сlosed problem of plasticity theory. Journal of Chemical Technology and Metallurgy, 56 (4), 867–876.
- Timoshenko, S. P., Guder, Dzh. (1979). Teoriia uprugosti. Moscow: Nauka, 560.
- Dorofeyev, O. A., Kovtun, V. V. (2019). Estimation of the Stress-Strain State of a Discrete Medium by a Plastic Flow Model. Problems of tribology, 93 (3), 29–38. doi: https://doi.org/10.31891/2079-1372-2019-93-3-29-38
- Andersen, R. G., Londono, J. G., Woelke, P. B., Nielsen, K. L. (2020). Fundamental differences between plane strain bending and far-field plane strain tension in ductile plate failure. Journal of the Mechanics and Physics of Solids, 141. doi: https://doi.org/10.1016/j.jmps.2020.103960
- Stampouloglou, I. H., Theotokoglou, E. E. (2009). Additional Separated-Variable Solutions of the Biharmonic Equation in Polar Coordinates. Journal of Applied Mechanics, 77 (2). doi: https://doi.org/10.1115/1.3197157
- El-Naaman, S. A., Nielsen, K. L., Niordson, C. F. (2019). An investigation of back stress formulations under cyclic loading. Mechanics of Materials, 130, 76–87. doi: https://doi.org/10.1016/j.mechmat.2019.01.005
- Lopez-Crespo, P., Camas, D., Antunes, F. V., Yates, J. R. (2018). A study of the evolution of crack tip plasticity along a crack front. Theoretical and Applied Fracture Mechanics, 98, 59–66. doi: https://doi.org/10.1016/j.tafmec.2018.09.012
- Li, J., Zhang, Z., Li, C. (2017). Elastic-plastic stress-strain calculation at notch root under monotonic, uniaxial and multiaxial loadings. Theoretical and Applied Fracture Mechanics, 92, 33–46. doi: https://doi.org/10.1016/j.tafmec.2017.05.005
- Pathak, H. (2017). Three-dimensional quasi-static fatigue crack growth analysis in functionally graded materials (FGMs) using coupled FE-XEFG approach. Theoretical and Applied Fracture Mechanics, 92, 59–75. doi: https://doi.org/10.1016/j.tafmec.2017.05.010
- Correia, J. A. F. O., Huffman, P. J., De Jesus, A. M. P., Cicero, S., Fernández-Canteli, A., Berto, F., Glinka, G. (2017). Unified two-stage fatigue methodology based on a probabilistic damage model applied to structural details. Theoretical and Applied Fracture Mechanics, 92, 252–265. doi: https://doi.org/10.1016/j.tafmec.2017.09.004
- Kovalevska, I., Samusia, V., Kolosov, D., Snihur, V., Pysmenkova, T. (2020). Stability of the overworked slightly metamorphosed massif around mine working. Mining of Mineral Deposits, 14 (2), 43–52. doi: https://doi.org/10.33271/mining14.02.043
- Sinekop, N. S., Lobanova, L. S., Parkhomenko, L. A. (2015). Metod R–funktcii v dinamicheskikh zadachakh teorii uprugosti. Kharkiv: KhGUPT, 95.
- Hussein, N. S. (2014). Solution of a Problem Linear Plane Elasticity with Mixed Boundary Conditions by the Method of Boundary Integrals. Mathematical Problems in Engineering, 2014, 1–11. doi: https://doi.org/10.1155/2014/323178
- Chigirinsky, V., Putnoki, A. (2017). Development of a dynamic model of transients in mechanical systems using argument-functions. Eastern-European Journal of Enterprise Technologies, 3 (7 (87)), 11–22. doi: https://doi.org/10.15587/1729-4061.2017.101282
- Chigirinsky, V., Naumenko, O. (2019). Studying the stressed state of elastic medium using the argument functions of a complex variable. Eastern-European Journal of Enterprise Technologies, 5 (7 (101)), 27–35. doi: https://doi.org/10.15587/1729-4061.2019.177514
- Chigirinsky, V., Naumenko, O. (2020). Invariant differential generalizations in problems of the elasticity theory as applied to polar coordinates. Eastern-European Journal of Enterprise Technologies, 5 (7 (107)), 56–73. doi: https://doi.org/10.15587/1729-4061.2020.213476
- Chigirinsky, V., Naumenko, O. (2021). Advancing a generalized method for solving problems of continuum mechanics as applied to the Cartesian coordinate system. Eastern-European Journal of Enterprise Technologies, 5 (7 (113)), 14–24. doi: https://doi.org/10.15587/1729-4061.2021.241287
- Tcelikov, A. I. (1962). Teoriia rascheta usilii v prokatnykh stanakh. Moscow: Metallurgizdat, 494.
- Arkulis, G. E., Dorogobid, V. G. (1987). Teoriia plastichnosti. Moscow: Metallurgiia, 251.
- Tikhonov, A. N., Samarskii, A. A. (1999). Uravneniia matematicheskoi fiziki. Moscow: Izd-vo MGU, 799.
- Muskhelishvili, N. I. (1966). Nekotorye osnovnye zadachi matematicheskoi teorii uprugosti. Moscow: Nauka, 709.
- Kolmogorov, V. L. (1970). Napriazheniia, deformatcii, razrusheniia. Moscow: Metallurgiia, 230.
- Klimenko, P. L. (2007). Kontaktnye napriazheniia pri prokatke. Dnepropetrovsk: POROGI, 285.
- Pozdeev, A. A., Tarnovskii, V. I. (1959). O raschete konechnykh peremeshchenii po ikh prirashcheniiam pri OMD. Izvestiia vuzov. Chernaia metallurgiia, 6, 43–52.
- Chigirinsky, V., Naizabekov, A., Lezhnev, S., Kuzmin, S., Naumenko, O. (2022). Solving applied problems of elasticity theory in geomechanics using the method of argument functions of a complex variable. Eastern-European Journal of Enterprise Technologies, 5 (7 (119)), 105–113. doi: https://doi.org/10.15587/1729-4061.2022.265673
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2023 Valeriy Chigirinsky, Abdrakhman Naizabekov, Sergey Lezhnev, Olena Naumenko, Sergey Kuzmin

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.









