Визначення закономірностей асиметрічної взаємодії пластичного середовища з протиспрямованою течією металу

Автор(и)

DOI:

https://doi.org/10.15587/1729-4061.2024.293842

Ключові слова:

асиметрія навантаження, протиспрямована течія металу, плоска задача, ефекти пластичного деформування

Анотація

Аналітично вирішена плоска задача теорії прокатки з використанням методу аргумент функцій комплексної змінної. Показано розв'язання задачі з погляду асиметрії, протиспрямованої течії металу, взаємодії зон в осередку деформації. Запропонована фізична модель дозволяє визначити вплив різних факторів на силові та деформаційні параметрі процесу, охарактеризувати особливості пластичної формозміни в єдиному осередку деформування з боку зон відставання та випередження.

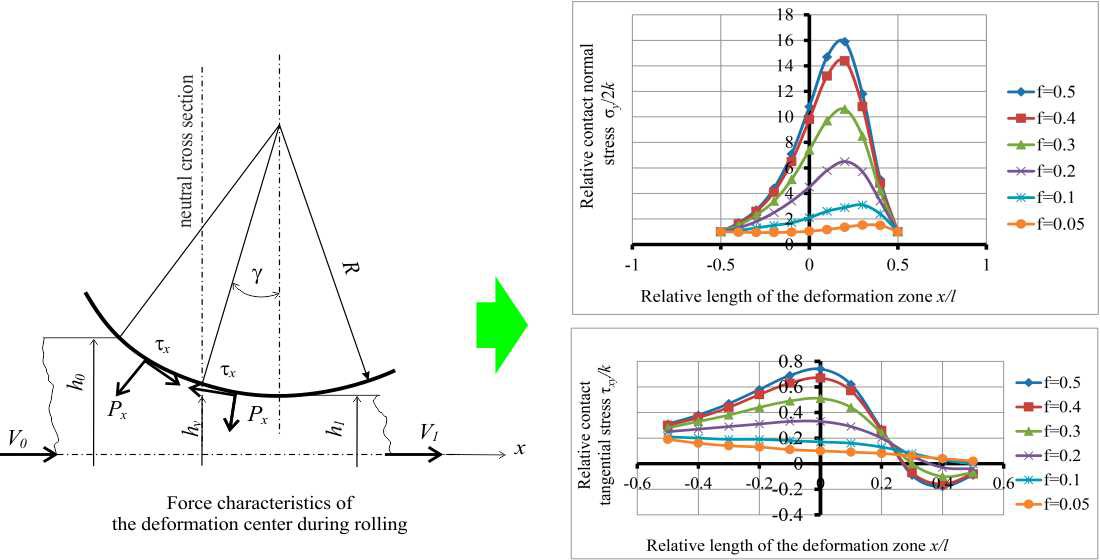
Ефекти пластичного деформування доводять, що взаємодія зон з протиспрямованої течією металу може бути фактором змін в осередку обтиску. Проаналізовано напружений стан проміжних схем навантаження. Доведено, що стійкість процесу прокатки (відсутність пробуксовки) визначається факторами: форма осередку деформації, контактне тертя, кут захоплення, умови реалізації захоплюючою здатністю валків.

Використання математичної моделі процесу дозволяє детальніше розглянути переходи в осередку деформації з наочним поданням епюр контактних напружень. З'являється наочна можливість оцінки захоплюючої здатності валків по епюрах нормальних та дотичних напружень від локальних параметрів процесу.

Показано, що взаємодія зон з протилежним перебігом металу є аналогом дії заднього розтягувального напруження за всіма параметрами впливу на процес формозміни. Проведені дослідження підтверджують загальноприйняті положення теорії прокатки, але виявляють ефекти пластичного деформування в умовах різного напруженого стану за рахунок різних режимів навантаження. Виявлена зона досяжності лімітованого осередку деформації.

Результати роботи дозволяють виявити ефекти пластичної деформації зі зниженням загального зусилля в процесах, які знаходяться в зонах досяжності лімітного осередку обтиску в умовах зростанні кінематичного навантаження при зміні кутів захоплення в межах 0,077…0,168

Біографії авторів

Valeriy Chigirinsky, Rudny Industrial Institute

Doctor of Technical Sciences, Professor

Department of Metallurgy and Mining

Abdrakhman Naizabekov, Rudny Industrial Institute

Doctor of Technical Sciences, Professor, Chairman of the Management Board-Rector

Department of Metallurgy and Mining

Sergey Lezhnev, Rudny Industrial Institute

PhD, Associate Professor

Department of Metallurgy and Mining

Олена Геннадіївна Науменко, Національний технічний університет «Дніпровська політехніка»

Старший викладач

Кафедра механічної та біомедичної інженерії

Sergey Kuzmin, Rudny Industrial Institute

PhD

Department of Metallurgy and Mining

Посилання

  1. Maksymenko, O. P., Loboiko, D. Y., Shtoda, M. N., Shtoda, Y. Y. (2018). Issledovanie prodolnoi ustoichivosti polosy pri prokatke na nepreryvnykh stanakh. Zbirnyk naukovykh prats Dniprovskoho derzhavnoho tekhnichnoho universytetu. Tekhnichni nauky. Tem. vyp., 59–64.
  2. Maksimenko, O. P., Romaniuk, R. Ia. (2009). Analiz prodolnoi ustoichivosti protcessa prokatki s uchetom vnutrennikh sil i rezhima natiazheniia polosy. Izvestiia vuzov. Chernaia metallurgiia, 10, 32–34.
  3. Grudev, A. P. (1998). Zakhvatyvaiushchaia sposobnost prokatnykh valkov. Moscow: SP Intermet Inzhiniring, 283.
  4. Ryabov, P. N. (2017). The features of plastic flow localization in materials under shear deformations. AIP Conference Proceedings. doi: https://doi.org/10.1063/1.4992562
  5. Vabishchevich, M., Zatyliuk, G. (2021). Analysis of the stressed-strained state of the foundation-shell at interaction with the elastic-plastic medium. Strength of Materials and Theory of Structures, 106, 105–112. doi: https://doi.org/10.32347/2410-2547.2021.106.105-112
  6. Solodei, I., Petrenko, E., Zatyliuk, G. (2020). Nonlinear problem of structural deformation in interaction with elastoplastic medium. Strength of Materials and Theory of Structures, 105, 48–63. doi: https://doi.org/10.32347/2410-2547.2020.105.48-63
  7. Rogov, Ye. I., Kussainov, A. A., Gumenyuk, V. V. (2018). Physical models of solid mass and related processes in interaction with foundations. Journal of Mechanical Engineering Research & Developments, 41 (2), 65–74. doi: https://doi.org/10.26480/jmerd.02.2018.65.74
  8. Vasidzu, K. (1987). Variatcionnye metody v teorii uprugosti i plastichnosti. Moscow: Mir, 542.
  9. Kolmogorov, V. L. (1986). Mekhanika obrabotki metallov davleniem. Moscow: Metallurgiia, 686.
  10. Gun, G. Ia. (1980). Teoreticheskie osnovy obrabotki metallov davleniem. Moscow: Metallurgiia, 456.
  11. Tarnovskii, I. Ia., Pozdeev, A. A., Ganago, O. A. et al. (1963). Teoriia obrabotki metallov davleniem. Moscow: Metallurgizdat, 673.
  12. Zubchaninov, V. G. (2002). Matematicheskaia teoriia plastichnosti. Tver: TGTU, 300.
  13. Krysko, A. V., Papkova, I. V., Rezchikov, A. F., Krysko, V. A. (2022). A New Mathematical Model of Functionally Graded Porous Euler–Bernoulli Nanoscaled Beams Taking into Account Some Types of Nonlinearities. Materials, 15 (20), 7186. doi: https://doi.org/10.3390/ma15207186
  14. Bondar, V. S., Danshin, V. V. (2008). Plastichnost. Proportcionalnye i neproportcionalnye nagruzheniia. Moscow: Fizmatlit, 176.
  15. Chigirinsky, V., Naizabekov, A., Lezhnev, S. (2021). Сlosed problem of plasticity theory. Journal of Chemical Technology and Metallurgy, 56 (4), 867–876.
  16. Timoshenko, S. P., Guder, Dzh. (1979). Teoriia uprugosti. Moscow: Nauka, 560.
  17. Dorofeyev, O. A., Kovtun, V. V. (2019). Estimation of the Stress-Strain State of a Discrete Medium by a Plastic Flow Model. Problems of tribology, 93 (3), 29–38. doi: https://doi.org/10.31891/2079-1372-2019-93-3-29-38
  18. Andersen, R. G., Londono, J. G., Woelke, P. B., Nielsen, K. L. (2020). Fundamental differences between plane strain bending and far-field plane strain tension in ductile plate failure. Journal of the Mechanics and Physics of Solids, 141. doi: https://doi.org/10.1016/j.jmps.2020.103960
  19. Stampouloglou, I. H., Theotokoglou, E. E. (2009). Additional Separated-Variable Solutions of the Biharmonic Equation in Polar Coordinates. Journal of Applied Mechanics, 77 (2). doi: https://doi.org/10.1115/1.3197157
  20. El-Naaman, S. A., Nielsen, K. L., Niordson, C. F. (2019). An investigation of back stress formulations under cyclic loading. Mechanics of Materials, 130, 76–87. doi: https://doi.org/10.1016/j.mechmat.2019.01.005
  21. Lopez-Crespo, P., Camas, D., Antunes, F. V., Yates, J. R. (2018). A study of the evolution of crack tip plasticity along a crack front. Theoretical and Applied Fracture Mechanics, 98, 59–66. doi: https://doi.org/10.1016/j.tafmec.2018.09.012
  22. Li, J., Zhang, Z., Li, C. (2017). Elastic-plastic stress-strain calculation at notch root under monotonic, uniaxial and multiaxial loadings. Theoretical and Applied Fracture Mechanics, 92, 33–46. doi: https://doi.org/10.1016/j.tafmec.2017.05.005
  23. Pathak, H. (2017). Three-dimensional quasi-static fatigue crack growth analysis in functionally graded materials (FGMs) using coupled FE-XEFG approach. Theoretical and Applied Fracture Mechanics, 92, 59–75. doi: https://doi.org/10.1016/j.tafmec.2017.05.010
  24. Correia, J. A. F. O., Huffman, P. J., De Jesus, A. M. P., Cicero, S., Fernández-Canteli, A., Berto, F., Glinka, G. (2017). Unified two-stage fatigue methodology based on a probabilistic damage model applied to structural details. Theoretical and Applied Fracture Mechanics, 92, 252–265. doi: https://doi.org/10.1016/j.tafmec.2017.09.004
  25. Kovalevska, I., Samusia, V., Kolosov, D., Snihur, V., Pysmenkova, T. (2020). Stability of the overworked slightly metamorphosed massif around mine working. Mining of Mineral Deposits, 14 (2), 43–52. doi: https://doi.org/10.33271/mining14.02.043
  26. Sinekop, N. S., Lobanova, L. S., Parkhomenko, L. A. (2015). Metod R–funktcii v dinamicheskikh zadachakh teorii uprugosti. Kharkiv: KhGUPT, 95.
  27. Hussein, N. S. (2014). Solution of a Problem Linear Plane Elasticity with Mixed Boundary Conditions by the Method of Boundary Integrals. Mathematical Problems in Engineering, 2014, 1–11. doi: https://doi.org/10.1155/2014/323178
  28. Chigirinsky, V., Putnoki, A. (2017). Development of a dynamic model of transients in mechanical systems using argument-functions. Eastern-European Journal of Enterprise Technologies, 3 (7 (87)), 11–22. doi: https://doi.org/10.15587/1729-4061.2017.101282
  29. Chigirinsky, V., Naumenko, O. (2019). Studying the stressed state of elastic medium using the argument functions of a complex variable. Eastern-European Journal of Enterprise Technologies, 5 (7 (101)), 27–35. doi: https://doi.org/10.15587/1729-4061.2019.177514
  30. Chigirinsky, V., Naumenko, O. (2020). Invariant differential generalizations in problems of the elasticity theory as applied to polar coordinates. Eastern-European Journal of Enterprise Technologies, 5 (7 (107)), 56–73. doi: https://doi.org/10.15587/1729-4061.2020.213476
  31. Chigirinsky, V., Naumenko, O. (2021). Advancing a generalized method for solving problems of continuum mechanics as applied to the Cartesian coordinate system. Eastern-European Journal of Enterprise Technologies, 5 (7 (113)), 14–24. doi: https://doi.org/10.15587/1729-4061.2021.241287
  32. Tcelikov, A. I. (1962). Teoriia rascheta usilii v prokatnykh stanakh. Moscow: Metallurgizdat, 494.
  33. Arkulis, G. E., Dorogobid, V. G. (1987). Teoriia plastichnosti. Moscow: Metallurgiia, 251.
  34. Tikhonov, A. N., Samarskii, A. A. (1999). Uravneniia matematicheskoi fiziki. Moscow: Izd-vo MGU, 799.
  35. Muskhelishvili, N. I. (1966). Nekotorye osnovnye zadachi matematicheskoi teorii uprugosti. Moscow: Nauka, 709.
  36. Kolmogorov, V. L. (1970). Napriazheniia, deformatcii, razrusheniia. Moscow: Metallurgiia, 230.
  37. Klimenko, P. L. (2007). Kontaktnye napriazheniia pri prokatke. Dnepropetrovsk: POROGI, 285.
  38. Pozdeev, A. A., Tarnovskii, V. I. (1959). O raschete konechnykh peremeshchenii po ikh prirashcheniiam pri OMD. Izvestiia vuzov. Chernaia metallurgiia, 6, 43–52.
  39. Chigirinsky, V., Naizabekov, A., Lezhnev, S., Kuzmin, S., Naumenko, O. (2022). Solving applied problems of elasticity theory in geomechanics using the method of argument functions of a complex variable. Eastern-European Journal of Enterprise Technologies, 5 (7 (119)), 105–113. doi: https://doi.org/10.15587/1729-4061.2022.265673
Визначення закономірностей асиметрічної взаємодії пластичного середовища з протиспрямованою течіею металу

##submission.downloads##

Опубліковано

2024-02-28

Як цитувати

Chigirinsky, V., Naizabekov, A., Lezhnev, S., Науменко, О. Г., & Kuzmin, S. (2024). Визначення закономірностей асиметрічної взаємодії пластичного середовища з протиспрямованою течією металу. Eastern-European Journal of Enterprise Technologies, 1(7 (127), 66–82. https://doi.org/10.15587/1729-4061.2024.293842

Номер

Том 1 № 7 (127) (2024): Прикладна механіка

Розділ

Прикладна механіка

Ліцензія

Авторське право (c) 2023 Valeriy Chigirinsky, Abdrakhman Naizabekov, Sergey Lezhnev, Olena Naumenko, Sergey Kuzmin

Creative Commons License

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.

Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.

Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.