Optimizing the uncertainty of measurements on a coordinate measuring machine when controlling complex geometric surfaces
DOI:
https://doi.org/10.15587/1729-4061.2024.310051Keywords:
coordinate measuring machine, uncertainty optimization, complex geometric surfaces, adaptive measurement strategy, measurement uncertainty, Monte Carlo method, quality control, industrial metrology, measurement automation, high-precision manufacturingAbstract
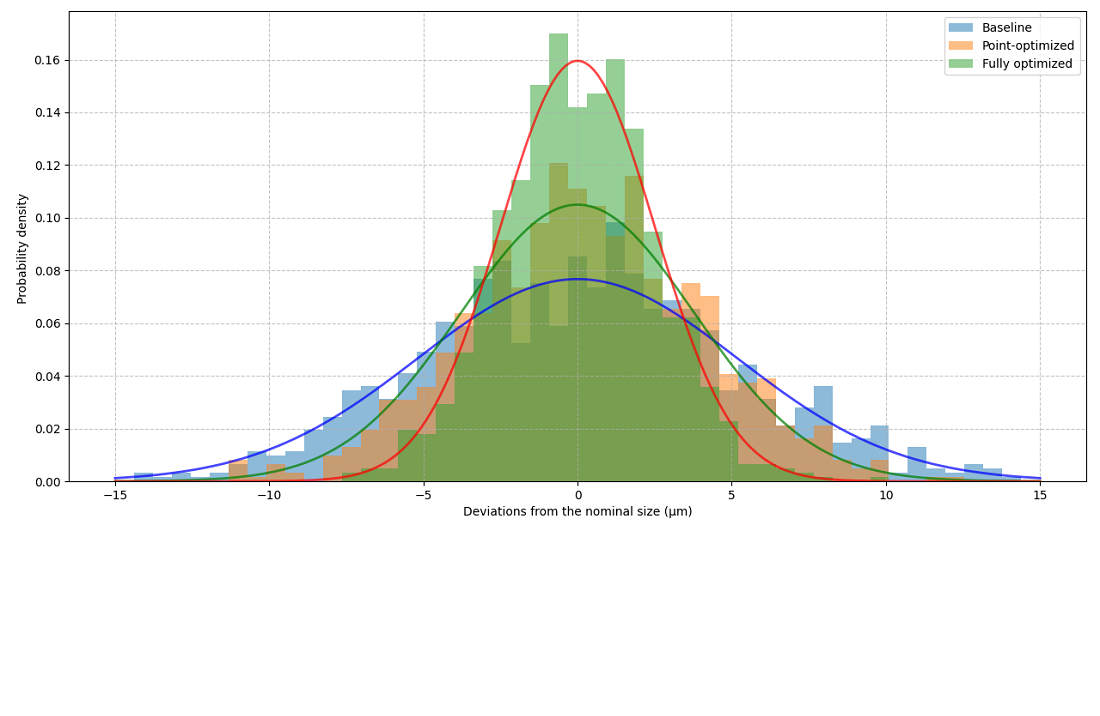
The object of this study is the process of optimizing measurement uncertainty on a coordinate measuring machine (CMM) when inspecting complex geometric surfaces. The problem addressed was insufficient accuracy and efficiency of measurements of complex parts on CMMs under production conditions. A method for optimizing measurement uncertainty has been devised, which includes a mathematical model of the measurement process and an adaptive algorithm for optimizing the control strategy, based on the Monte Carlo method. The model takes into account the geometry of surfaces and CMM characteristics, while the algorithm dynamically adjusts measurement parameters. The results demonstrate a reduction in measurement uncertainty by 15–20 % and a reduction in inspection time by 10–12 % compared to conventional methods. This is achieved by taking into account the specificity of complex surface geometry and an adaptive approach.
The uniqueness of the developed method is the ability to automatically adapt to different types of CMMs and measured objects, optimizing the number and location of measurement points, the speed of probe movement, and its contact force with the surface. The method takes into account not only the geometric parameters of objects but also the characteristics of the CMM itself, which allows for high accuracy. The method is particularly effective for parts with complex geometry, in which conventional methods often lead to significant errors.
Practical application is possible at machine-building enterprises for quality control of complex parts, especially in serial production. The implementation of the developed method allows for improving product quality and reducing production costs by 8–10 % due to optimization of the control process and reduction of defects
References
- Liao, Z.-Y., Wang, Q.-H., Xu, Z.-H., Wu, H.-M., Li, B., Zhou, X.-F. (2024). Uncertainty-aware error modeling and hierarchical redundancy optimization for robotic surface machining. Robotics and Computer-Integrated Manufacturing, 87, 102713. https://doi.org/10.1016/j.rcim.2023.102713
- Ziętarski, S., Kachel, S., Benaouali, A. (2016). Coordinate measuring machine uncertainty analysis using the combinatorial cyclic method of optimization. Mechanik, 7, 876–877. https://doi.org/10.17814/mechanik.2016.7.216
- Zhao, X., Ji, L., Zhao, L. (2018). Calibration of Parallelism Error About Rotating Shafts Based on the Three-coordinate Measuring Machine. Proceedings of the 2nd International Conference on Intelligent Manufacturing and Materials. https://doi.org/10.5220/0007532203790383
- Shen, M., Yang, H., Chang, D., Jiang, X., Hu, Y. (2024). Dynamic error modeling and analysis of articulated arm coordinate measuring machine with integrated joint module. Measurement Science and Technology, 35 (6), 065022. https://doi.org/10.1088/1361-6501/ad35de
- Cheung, C., Ren, M., Kong, L., Whitehouse, D. (2014). Modelling and analysis of uncertainty in the form characterization of ultra-precision freeform surfaces on coordinate measuring machines. CIRP Annals, 63 (1), 481–484. https://doi.org/10.1016/j.cirp.2014.03.032
- Zhuang, Q., Wan, N., Guo, Y., Zhu, G., Qian, D. (2024). A state-of-the-art review on the research and application of on-machine measurement with a touch-trigger probe. Measurement, 224, 113923. https://doi.org/10.1016/j.measurement.2023.113923
- Wojtyła, M., Rosner, P., Płowucha, W., Forbes, A. B., Savio, E., Balsamo, A. (2022). Validation of the sensitivity analysis method of coordinate measurement uncertainty evaluation. Measurement, 199, 111454. https://doi.org/10.1016/j.measurement.2022.111454
- Zhang, M., Liu, D., Liu, Y. (2024). Recent progress in precision measurement and assembly optimization methods of the aero-engine multistage rotor: A comprehensive review. Measurement, 235, 114990. https://doi.org/10.1016/j.measurement.2024.114990
- Wozniak, A., Krajewski, G., Byszewski, M. (2019). A new method for examining the dynamic performance of coordinate measuring machines. Measurement, 134, 814–819. https://doi.org/10.1016/j.measurement.2018.12.041
- Hu, Y., Zhao, R., Ju, B. (2021). Geometric analysis of measurement errors in a surface metrology class with closed-loop probes. Measurement, 184, 109869. https://doi.org/10.1016/j.measurement.2021.109869
- Yan, Y., He, G., Sang, Y., Yao, C., Wang, S., Chen, F. (2022). A two-module automated scanning inspection planning methodology for complex surfaces on coordinate measuring machine. Measurement, 202, 111827. https://doi.org/10.1016/j.measurement.2022.111827
- Xing, T., Zhao, X., Song, L., Cui, Z., Zou, X., Sun, T. (2022). On-machine measurement method and geometrical error analysis in a multi-step processing system of an ultra-precision complex spherical surface. Journal of Manufacturing Processes, 80, 161–177. https://doi.org/10.1016/j.jmapro.2022.05.057
- Sato, O., Takatsuji, T., Matsuzaki, K., Watanabe, M., Kajima, M., Miura, Y., Nakanishi, S. (2024). Practical experimental design and uncertainty evaluation method for dimensional and form measurements using coordinate measuring machines. Measurement, 227, 114224. https://doi.org/10.1016/j.measurement.2024.114224
- Ren, M., Cheung, C., Kong, L., Wang, S. (2015). Quantitative Analysis of the Measurement Uncertainty in Form Characterization of Freeform Surfaces Based on Monte Carlo Simulation. Procedia CIRP, 27, 276–280. https://doi.org/10.1016/j.procir.2015.04.078
- Wang, Z., He, X., Wang, Y. (2021). Different measuring methods of REVO five-axis coordinate measuring machine. Tenth International Symposium on Precision Mechanical Measurements. https://doi.org/10.1117/12.2613428
- Internet-Based Surface Metrology Algorithm Testing System. National Institute of Standards and Technology. Available at: https://physics.nist.gov/VSC/jsp/About.jsp
- D Metrology Use Cases. GOM GmbH.
- Example Studies. Digital Surf. Available at: https://www.digitalsurf.com/
- An opensource on-machine 3D Scanner CMM (Coordinate Measuring Machine) system. OpenCMM. Available at: https://github.com/OpenCMM/OpenCMM
- Sousa, A. R. (2018). Metrological evaluation of a Coordinate Measuring Machine with 5-axis measurement technology. Procedia CIRP, 75, 367–372. https://doi.org/10.1016/j.procir.2018.04.035
- Nasir, S. S. M., Hussin, N., Fohimi, N. A. M., Ibrahim, D., Wahab, R. M. (2023). Design Improvement and Fabrication of a Jig for Holding a Workpiece in a Coordinate Measuring Machine. Progress in Engineering Technology V, 197–206. https://doi.org/10.1007/978-3-031-29348-1_21
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2024 Volodymyr Kvasnikov, Oleg Chalyi, Maryna Graf, Anatolii Perederko

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.









