Improving an analytical model of the near magnetic field of electromagnets in the spacecraft orientation control system

Authors

DOI:

https://doi.org/10.15587/1729-4061.2025.326676

Keywords:

magnetic field, analytical model, cylindrical electromagnet, magnetic purity, spacecraft

Abstract

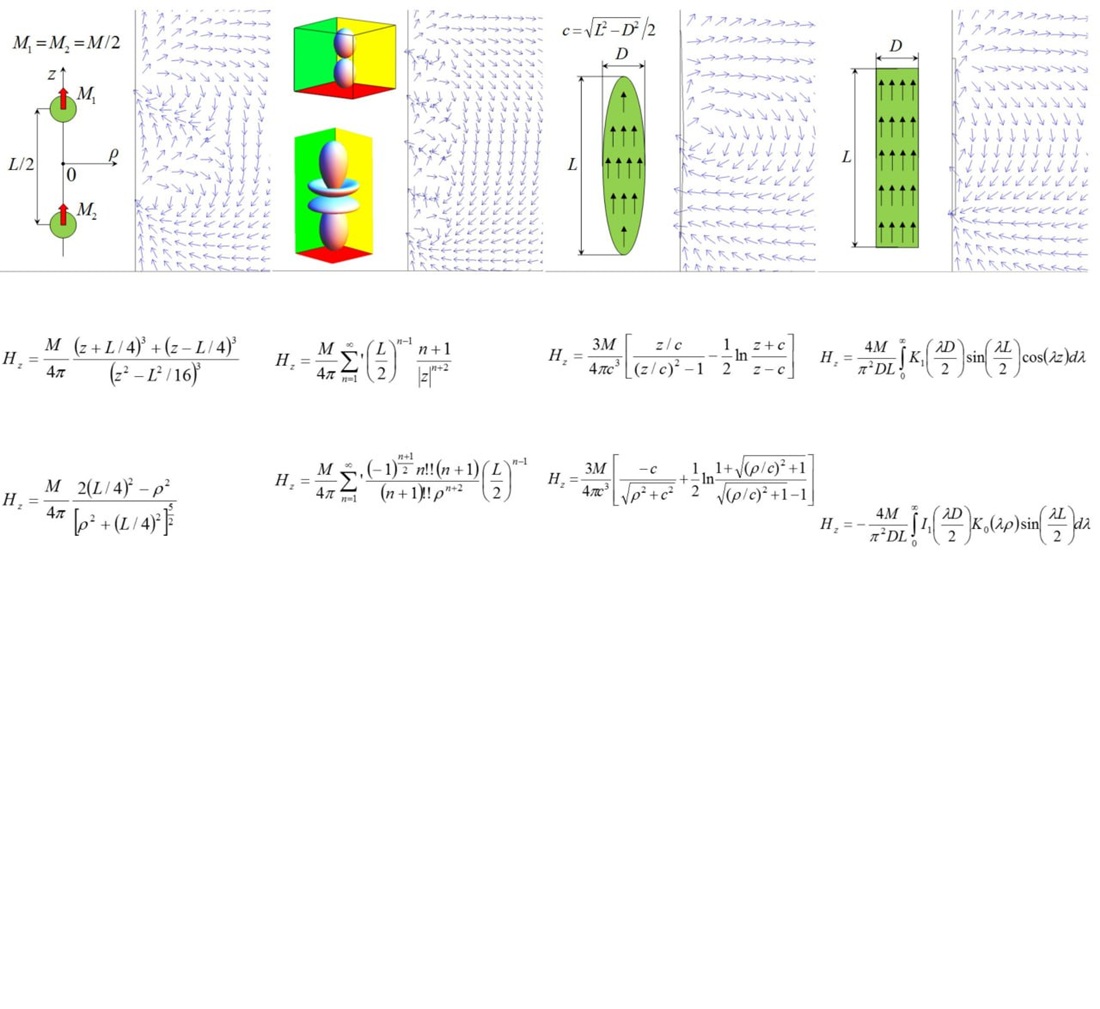
The specificity of applying the technology for ensuring magnetic purity of small spacecraft, which have cylindrical electromagnets with a magnetic moment of 10–50 A m2 in the orbit orientation control system, has been considered. It is shown that the electromagnets of the orientation control system are the most powerful source of magnetic hindrance with a magnetic flux density of up to 1 T for the magnetically sensitive equipment of the spacecraft. The need for modeling the magnetic field of the electromagnet at the preliminary stage of spacecraft development for the rational choice of its layout has been substantiated. In order to improve the technology for ensuring magnetic purity, which is aimed at increasing the reliability of spacecraft operation, a search for the best model of the magnetic field of such electromagnets was carried out.

A comparative analysis of approximate analytical models of the near magnetic field of a cylindrical electromagnet, which are based on its magnetic moment and overall dimensions, was carried out. It is established that the model based on two shifted dipole moments and the multipole model have unacceptably large deviations in the results of calculating the near magnetic field near the body of a cylindrical electromagnet. The advantages in the form of an expanded application area and a reduced deviation of the near magnetic field representation to 5 % when using the model based on cylindrical harmonics of the electromagnet have been theoretically substantiated. Formulas for engineering calculation of the magnetic field induced by a cylindrical electromagnet inside the spacecraft using its improved analytical model have been derived. It is proposed to use the model based on cylindrical harmonics for preliminary calculation of the magnetic hindrance generated by the electromagnets of the orientation control system to the magnetically sensitive equipment of the spacecraft

Author Biographies

Andriy Getman, National Technical University "Kharkiv Polytechnic Institute"

Doctor of Technical Sciences, Senior Researcher

Department of Theoretical Electrical Engineering

Oleksandr Konstantinov, National Technical University "Kharkiv Polytechnic Institute"

PhD Student

Department of Theoretical Electrical Engineering

References

  1. ECSS-E-HB-20-07A. Space engineering: Electromagnetic compatibility hand-book. ESA-ESTEC (2012). Noordwijk: Requirements & Standards Division, 228.
  2. ECSS-E-HB-20-07С Rev.2. Space engineering: Electromagnetic compatibility hand-book. ESA-ESTEC (2022). Noordwijk, 116.
  3. Weikert, S., Mehlem, K., Wiegand, A. (2012). Spacecraft magnetic cleanliness prediction and control. ESA Workshop on Aerospace EMC. Available at: https://www.researchgate.net/publication/241633435_Spacecraft_magnetic_cleanliness_prediction_and_control
  4. Connerney, J. E. P., Benn, M., Bjarno, J. B., Denver, T., Espley, J., Jorgensen, J. L. et al. (2017). The Juno Magnetic Field Investigation. Space Science Reviews, 213 (1-4), 39–138. https://doi.org/10.1007/s11214-017-0334-z
  5. Lee, J., Jin, H., Kim, K.-H., Park, H., Jo, W., Jang, Y. et al. (2023). Correction of Spacecraft Magnetic Field Noise: Initial Korean Pathfinder Lunar Orbiter MAGnetometer Observation in Solar Wind. Sensors, 23 (23), 9428. https://doi.org/10.3390/s23239428
  6. de Soria-Santacruz, M., Soriano, M., Quintero, O., Wong, F., Hart, S., Kokorowski, M. et al. (2020). An Approach to Magnetic Cleanliness for the Psyche Mission. 2020 IEEE Aerospace Conference, 1–15. https://doi.org/10.1109/aero47225.2020.9172801
  7. Arranz, C. J., Marchese, V., Léger, J.-M., Vallmitjana, M., Jager, T., Pous, M. (2023). Magnetic cleanliness on NanoMagSat, a CubeSats’ constellation science mission. 2023 International Symposium on Electromagnetic Compatibility – EMC Europe, 1–6. https://doi.org/10.1109/emceurope57790.2023.10274205
  8. Park, H. H., Jin, H., Kim, T. Y., Kim, K. H., Lee, H. J., Shin, J. H. et al. (2022). Analysis of the KPLO magnetic cleanliness for the KMAG instrument. Advances in Space Research, 69 (2), 1198–1204. https://doi.org/10.1016/j.asr.2021.11.015
  9. Mentges, A., Rawal, B. S. (2022). Magnetic Dipole Moment Estimation from Nearfield Measurements Using Stochastic Gradient Descent AI Model. 2022 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COM-IT-CON), 327–332. https://doi.org/10.1109/com-it-con54601.2022.9850855
  10. Busch, S., Koss, P. A., Horch, C., Schäfer, K., Schimmerohn, M., Schäfer, F., Kühnemann, F. (2023). Magnetic cleanliness verification of miniature satellites for high precision pointing. Acta Astronautica, 210, 243–252. https://doi.org/10.1016/j.actaastro.2023.05.017
  11. Dorman, C. J., Piker, C., Miles, D. M. (2024). Automated static magnetic cleanliness screening for the TRACERS small-satellite mission. Geoscientific Instrumentation, Methods and Data Systems, 13 (1), 43–50. https://doi.org/10.5194/gi-13-43-2024
  12. Pudney, M. A., Carr, C. M., Schwartz, S. J., Howarth, S. I. (2013). Near-magnetic-field scaling for verification of spacecraft equipment. Geoscientific Instrumentation, Methods and Data Systems, 2 (2), 249–255. https://doi.org/10.5194/gi-2-249-2013
  13. Getman, A. (2023). Improving the technology for ensuring the magnetic cleanliness of small spacecraft. Eastern-European Journal of Enterprise Technologies, 3 (5 (123)), 33–42. https://doi.org/10.15587/1729-4061.2023.282444
  14. Lassakeur, A., Underwood, C. (2019). Magnetic Cleanliness Program on CubeSats for Improved Attitude Stability. 2019 9th International Conference on Recent Advances in Space Technologies (RAST), 123–129. https://doi.org/10.1109/rast.2019.8767816
  15. Belsten, N. (2022). Magnetic Cleanliness, Sensing, and Calibration for CubeSats. Massachusetts Institute of Technology. Available at: https://dspace.mit.edu/handle/1721.1/143167
  16. Vanderlinde, J. (2005). Classical Electromagnetic Theory. Springer Netherlands. https://doi.org/10.1007/1-4020-2700-1
  17. Smythe, W. (1989). Static and Dynamic Electricity. Hemisphere Publishing Corporation, 623.
  18. Getman, A. V., Konstantinov, A. V. (2013). Cylindrical harmonics of magnetic field of linear magnetized cylinder. Technical Electrodynamics, 1, 3–8. Available at: http://dspace.nbuv.gov.ua/handle/123456789/62253
Improving an analytical model of the near magnetic field of electromagnets in the spacecraft orientation control system

Downloads

Published

2025-04-30

How to Cite

Getman, A., & Konstantinov, O. (2025). Improving an analytical model of the near magnetic field of electromagnets in the spacecraft orientation control system. Eastern-European Journal of Enterprise Technologies, 2(5 (134), 6–14. https://doi.org/10.15587/1729-4061.2025.326676

Issue

Vol. 2 No. 5 (134) (2025): Applied physics

Section

Applied physics

License

Copyright (c) 2025 Andriy Getman, Oleksandr Konstantinov

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.