Конструювання плоскої заготовки для виготовлення витка прямого гелікоїда
DOI:
https://doi.org/10.15587/1729-4061.2023.275508Ключові слова:
прямий закритий гелікоїд, плоска заготовка, неперервне згинання, параметричні рівнянняАнотація
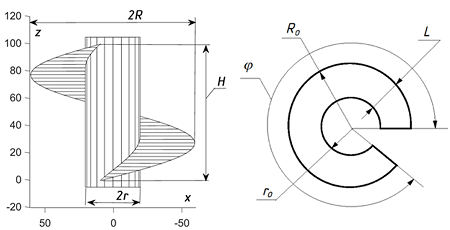
У техніці поширеною гвинтовою поверхнею є прямий закритий гелікоїд (шнек). Він утворюється гвинтовим рухом горизонтального відрізка за умови перетну осі шнека одним з його кінців. Утворення поверхні відкритого гелікоїда є аналогічним, проте відрізок при цьому має бути мимобіжним по відношенню до осі і розташованим на сталій відстані від неї. Із диференціальної геометрії відомо, що гвинтову поверхню можна перетворити шляхом згинання на поверхню обертання. Цей факт взято за основу розрахунку геометричної форми плоскої заготовки. Поверхня відкритого гелікоїда є нерозгортною, тому форма заготовки повинна бути знайдена таким чином, щоб звести до мінімуму пластичні деформації при формуванні поверхні.
Отримано параметричні рівняння неперервного згинання витка відкритого гелікоїда у відсік однопорожнинного гіперболоїда обертання. Неперервне згинання можна уявити як поступову деформацію витка з одночасним зменшенням його кроку. Меридіаном гіперболоїда обертання є відповідна ділянка гіперболи. Відсік гіперболоїда пропонується апроксимувати поверхнею зрізаного конуса. Ця апроксимація буде більш точною на ділянці гіперболи, де вона асимптотично наближається до відрізка прямої. Після вибору конуса з’являється можливість визначити його розміри і побудувати його точну розгортку, оскільки конус є розгортною поверхнею. Побудована розгортка у вигляді плоского кільця із вирізаним сектором і буде шуканою плоскою заготовкою для формування із неї витка шнека.
Найбільш точно поверхню витка відкритого гелікоїда можна виготовити за допомогою штамповки заготовки отриманої форми. Для малосерійного виготовлення гвинтової поверхні відкритого гелікоїда плоскі кільця доцільно зварити між собою і при монтажі розтягувати вздовж вала з одночасним скручуванням навколо його осі. Точність отриманої поверхні залежатиме від точності апроксимації відсіка гіперболоїда обертання зрізаним конусом, на що і спрямована дана робота.
Посилання
- Sokolova, L. N. S., Infante, D. L. R., Vladimir, J. P., Ermakova, E. (2020). Helical surfaces and their application in engineering design. International journal of science and technology, 29 (2), 1839–1846. Available at: https://www.researchgate.net/publication/339600632_Helical_surfaces_and_their_application_in_engineering_design
- Drahan, A. P., Klendii, M. B. (2021). Substantiation of the design of the working body of the screw section of the combined tillage tool. Perspective technologies and devices, 18, 66–73. doi: https://doi.org/10.36910/6775-2313-5352-2021-18-10
- Albu, S. C. (2019). Simulation of Processing of a Helical Surface with the Aid of a Frontal-Cylindrical Milling Tool. Procedia Manufacturing, 32, 36–41. doi: https://doi.org/10.1016/j.promfg.2019.02.180
- Kubota, Y., Ludewig, M., Thiang, G. C. (2022). Delocalized Spectra of Landau Operators on Helical Surfaces. Communications in Mathematical Physics, 395 (3), 1211–1242. doi: https://doi.org/10.1007/s00220-022-04452-4
- Konopatskiy, E., Bezditnyi, A. (2021). Solid modeling of geometric objects in point calculus. CEUR Workshop Proceedingsthis link is disabled, 3027, 666–672. doi: https://doi.org/10.20948/graphicon-2021-3027-666-672
- Konopatskiy, E. V., Bezditnyi, A. A. (2022). The Problem of Visualizing Solid Models as a Three-Parameter Point Set. Scientific Visualization, 14 (2), 49–61. doi: https://doi.org/10.26583/sv.14.2.05
- Konopatskiy, E. V., Seleznev, I. V., Bezditnyi, A. A. (2022). The use of interpolation methods for modelling multifactor processes based on an experiment planning matrix. Journal of Physics: Conference Series, 2182 (1), 012005. doi: https://doi.org/10.1088/1742-6596/2182/1/012005
- Madumarov, K. H. (2022). Graphical methods for depicting prismatic closed helical surfaces (PZVP). International journal of social science & interdisciplinary research, 11 (11). Available at: https://www.gejournal.net/index.php/IJSSIR/article/view/1128
- Madumarov, K. H. (2021). Graphic methods of image and mathematical description of lobe closed helical surfaces. Nat. Volatiles & Essent. Oils, 8 (4), 2686–2694.
- Andrés, M.-P., Alicia, L.-M.; Viana, V., Murtinho, V., Xavier, J. (Eds.) (2020). Developable helicoids from cylindrical helix and its application as architectural surface. Thinking, Drawing, Modelling. Cham: Springer, 107–120. doi: https://doi.org/10.1007/978-3-030-46804-0_8
- Melnyk, V., Vlasovets, V., Konoplianchenko, I., Tarelnyk, V., Dumanchuk, M., Martsynkovskyy, V. et al. (2021). Developing a system and criteria for directed choice of technology to provide required quality of surfaces of flexible coupling parts for rotor machines. Journal of Physics: Conference Series, 1741 (1), 012030. doi: https://doi.org/10.1088/1742-6596/1741/1/012030
- Gaponova, O. P., Tarelnyk, V. B., Martsynkovskyy, V. S., Konoplianchenko, Ie. V., Melnyk, V. I., Vlasovets, V. M. et al. (2021). Combined Electrospark Running-in Coatings of Bronze Parts. Part 2. Distribution of Elements in a Surface Layer. Metallofizika i noveishie tekhnologii, 43 (9), 1155–1166. doi: https://doi.org/10.15407/mfint.43.09.1155
- Merticaru, V., Nagîț, G., Dodun, O., Merticaru, E., Rîpanu, M. I., Mihalache, A. M., Slătineanu, L. (2022). Influence of Machining Conditions on Micro-Geometric Accuracy Elements of Complex Helical Surfaces Generated by Thread Whirling. Micromachines, 13 (9), 1520. doi: https://doi.org/10.3390/mi13091520
- Tarelnyk, V. B., Gaponova, O. P., Konoplianchenko, Y. V. (2022). Electric-spark alloying of metal surfaces with graphite. Progress in Physics of Metalsthis, 23 (1), 27–58. doi: https://doi.org/10.15407/ufm.23.01.027
- Tarelnyk, V., Konoplianchenko, I., Gaponova, O., Radionov, O., Antoszewski, B., Kundera, C. et al. (2022). Application of wear-resistant nanostructures formed by ion nitridizing & electrospark alloying for protection of rolling bearing seat surfaces. IEEE 12th International Conference Nanomaterials: Applications & Properties (NAP). doi: https://doi.org/10.1109/nap55339.2022.9934739
- Kresan, T., Pylypaka, S., Ruzhylo, Z., Rogovskii, I., Trokhaniak, O. (2021). Rolling of a single-cavity hyperboloid of rotation on a helicoid on which it bends. Engineering Review, 41 (3), 106–114. doi: https://doi.org/10.30765/er.1563
- Hevko, I. B., Leshchuk, R. Ya., Hud, V. Z., Dmytriv, O. R., Dubyniak, T. S., Navrotska, T. D., Kruhlyk, O. A. (2019). Hnuchki hvyntovi konveiery: proiektuvannia, tekhnolohiia vyhotovlennia, eksperymentalni doslidzhennia. Ternopil: FOP Palianytsia V. A., 208. Available at: http://elartu.tntu.edu.ua/handle/lib/28927
- Anuriev, V. I. (1978). Dovidnyk konstruktora-mashynobudivnyka. Moscow: Mashynobuduvannia, 1846.
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2023 Tatiana Volina, Serhii Pylypaka , Vyacheslav Hropost, Tetiana Kresan, Oleksandr Zabolotnii

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.
Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.










