Construction of a flat workpiece for manufacturing a turn of the right helicoid
DOI:
https://doi.org/10.15587/1729-4061.2023.275508Keywords:
right closed helicoid, flat workpiece, continuous bending, parametric equationsAbstract
In technology, a common helical surface is a right closed helicoid (auger). It is formed by a helical movement of a horizontal segment, provided that the axis of the auger crosses at one of its ends. The formation of the surface of an open helicoid is similar but the segment must intersect the axis and be located at a constant distance from it. It is known from differential geometry that the helical surface can be transformed by bending to the surface of rotation. This fact is taken as the basis for calculating the geometric shape of a flat workpiece. The surface of the open helicoid is non-disjointed, so the shape of the workpiece must be found in such a way as to minimize plastic deformations during surface formation.
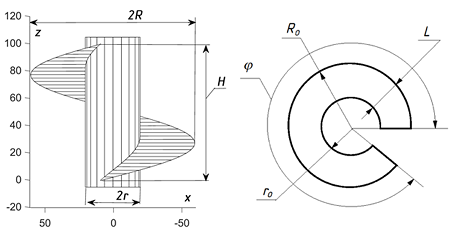
Parametric equations of continuous flexion of the turn of an open helicoid into the section of a single-cavity hyperboloid of rotation have been derived. Continuous bending can be represented as a gradual deformation of the turn while reducing its step. The meridian of hyperboloid rotation is the corresponding area of hyperbola. The hyperboloid section is proposed to be approximated by the surface of the truncated cone. This approximation will be more accurate in the area of the hyperbole where it asymptotically approaches the segment of the right line. After selecting a cone, it becomes possible to determine its size and build its exact sweep since the cone is a unfolding surface. The sweep is constructed in the form of a flat ring with a cut sector and will be the desired flat workpiece to form a turn of the auger from it.
Most accurately, the surface of the turn of the open helicoid can be made by stamping the workpiece of the resulting form. For small-scale production of the helical surface of an open helicoid, it is advisable to weld flat rings together and, during installation, stretch along the shaft while twisting around its axis. The accuracy of the obtained surface will depend on the accuracy of the approximation of the hyperboloid section of rotation with a truncated cone, which is the topic of this work.
References
- Sokolova, L. N. S., Infante, D. L. R., Vladimir, J. P., Ermakova, E. (2020). Helical surfaces and their application in engineering design. International journal of science and technology, 29 (2), 1839–1846. Available at: https://www.researchgate.net/publication/339600632_Helical_surfaces_and_their_application_in_engineering_design
- Drahan, A. P., Klendii, M. B. (2021). Substantiation of the design of the working body of the screw section of the combined tillage tool. Perspective technologies and devices, 18, 66–73. doi: https://doi.org/10.36910/6775-2313-5352-2021-18-10
- Albu, S. C. (2019). Simulation of Processing of a Helical Surface with the Aid of a Frontal-Cylindrical Milling Tool. Procedia Manufacturing, 32, 36–41. doi: https://doi.org/10.1016/j.promfg.2019.02.180
- Kubota, Y., Ludewig, M., Thiang, G. C. (2022). Delocalized Spectra of Landau Operators on Helical Surfaces. Communications in Mathematical Physics, 395 (3), 1211–1242. doi: https://doi.org/10.1007/s00220-022-04452-4
- Konopatskiy, E., Bezditnyi, A. (2021). Solid modeling of geometric objects in point calculus. CEUR Workshop Proceedingsthis link is disabled, 3027, 666–672. doi: https://doi.org/10.20948/graphicon-2021-3027-666-672
- Konopatskiy, E. V., Bezditnyi, A. A. (2022). The Problem of Visualizing Solid Models as a Three-Parameter Point Set. Scientific Visualization, 14 (2), 49–61. doi: https://doi.org/10.26583/sv.14.2.05
- Konopatskiy, E. V., Seleznev, I. V., Bezditnyi, A. A. (2022). The use of interpolation methods for modelling multifactor processes based on an experiment planning matrix. Journal of Physics: Conference Series, 2182 (1), 012005. doi: https://doi.org/10.1088/1742-6596/2182/1/012005
- Madumarov, K. H. (2022). Graphical methods for depicting prismatic closed helical surfaces (PZVP). International journal of social science & interdisciplinary research, 11 (11). Available at: https://www.gejournal.net/index.php/IJSSIR/article/view/1128
- Madumarov, K. H. (2021). Graphic methods of image and mathematical description of lobe closed helical surfaces. Nat. Volatiles & Essent. Oils, 8 (4), 2686–2694.
- Andrés, M.-P., Alicia, L.-M.; Viana, V., Murtinho, V., Xavier, J. (Eds.) (2020). Developable helicoids from cylindrical helix and its application as architectural surface. Thinking, Drawing, Modelling. Cham: Springer, 107–120. doi: https://doi.org/10.1007/978-3-030-46804-0_8
- Melnyk, V., Vlasovets, V., Konoplianchenko, I., Tarelnyk, V., Dumanchuk, M., Martsynkovskyy, V. et al. (2021). Developing a system and criteria for directed choice of technology to provide required quality of surfaces of flexible coupling parts for rotor machines. Journal of Physics: Conference Series, 1741 (1), 012030. doi: https://doi.org/10.1088/1742-6596/1741/1/012030
- Gaponova, O. P., Tarelnyk, V. B., Martsynkovskyy, V. S., Konoplianchenko, Ie. V., Melnyk, V. I., Vlasovets, V. M. et al. (2021). Combined Electrospark Running-in Coatings of Bronze Parts. Part 2. Distribution of Elements in a Surface Layer. Metallofizika i noveishie tekhnologii, 43 (9), 1155–1166. doi: https://doi.org/10.15407/mfint.43.09.1155
- Merticaru, V., Nagîț, G., Dodun, O., Merticaru, E., Rîpanu, M. I., Mihalache, A. M., Slătineanu, L. (2022). Influence of Machining Conditions on Micro-Geometric Accuracy Elements of Complex Helical Surfaces Generated by Thread Whirling. Micromachines, 13 (9), 1520. doi: https://doi.org/10.3390/mi13091520
- Tarelnyk, V. B., Gaponova, O. P., Konoplianchenko, Y. V. (2022). Electric-spark alloying of metal surfaces with graphite. Progress in Physics of Metalsthis, 23 (1), 27–58. doi: https://doi.org/10.15407/ufm.23.01.027
- Tarelnyk, V., Konoplianchenko, I., Gaponova, O., Radionov, O., Antoszewski, B., Kundera, C. et al. (2022). Application of wear-resistant nanostructures formed by ion nitridizing & electrospark alloying for protection of rolling bearing seat surfaces. IEEE 12th International Conference Nanomaterials: Applications & Properties (NAP). doi: https://doi.org/10.1109/nap55339.2022.9934739
- Kresan, T., Pylypaka, S., Ruzhylo, Z., Rogovskii, I., Trokhaniak, O. (2021). Rolling of a single-cavity hyperboloid of rotation on a helicoid on which it bends. Engineering Review, 41 (3), 106–114. doi: https://doi.org/10.30765/er.1563
- Hevko, I. B., Leshchuk, R. Ya., Hud, V. Z., Dmytriv, O. R., Dubyniak, T. S., Navrotska, T. D., Kruhlyk, O. A. (2019). Hnuchki hvyntovi konveiery: proiektuvannia, tekhnolohiia vyhotovlennia, eksperymentalni doslidzhennia. Ternopil: FOP Palianytsia V. A., 208. Available at: http://elartu.tntu.edu.ua/handle/lib/28927
- Anuriev, V. I. (1978). Dovidnyk konstruktora-mashynobudivnyka. Moscow: Mashynobuduvannia, 1846.
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2023 Tatiana Volina, Serhii Pylypaka , Vyacheslav Hropost, Tetiana Kresan, Oleksandr Zabolotnii

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.








