Determining the effect of additional tank volume and air pressure in the spring on the dynamic indicators of a pneumatic system of spring suspension in high-speed railroad rolling stock

Authors

DOI:

https://doi.org/10.15587/1729-4061.2024.304051

Keywords:

pneumatic spring suspension system, spring stiffness, damping coefficient, railroad rolling stock

Abstract

The object of this study is the pneumatic system in the spring suspension of rolling stock under conditions of high-speed movement from 170 to 250 km/h.

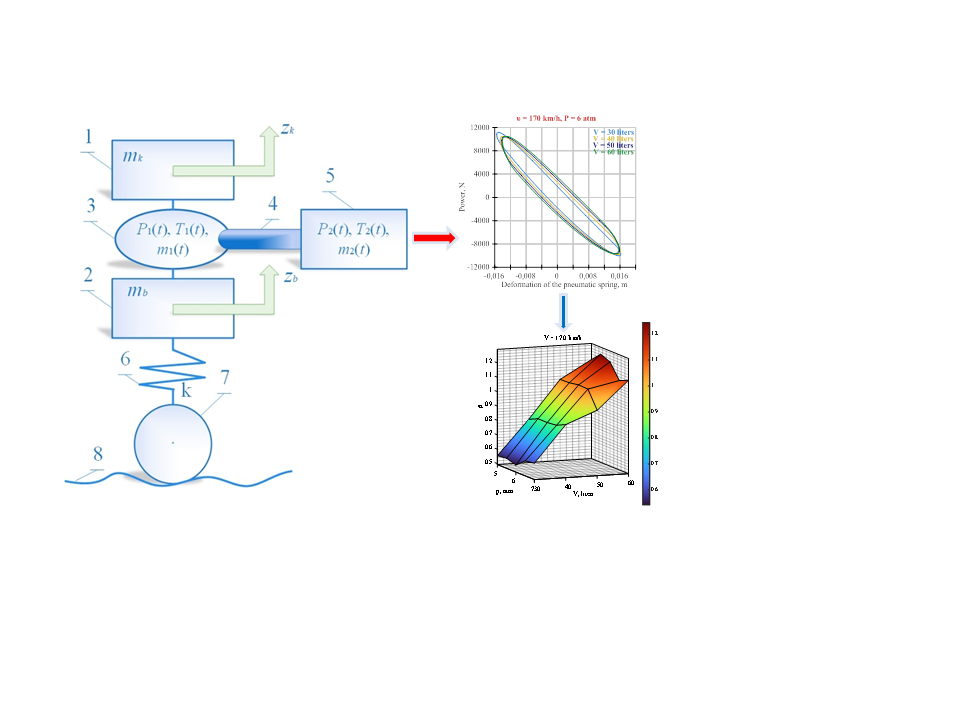
Based on the thermodynamic model of the pneumatic spring suspension system, the influence of volume of the additional tank and the initial pressure in the pneumatic spring on the nature of change in the spring's dynamic stiffness, energy losses, and damping coefficient was studied.

Based on the built "force-deformation" dependences for the pneumatic spring, it was established that the change in the volume of an additional tank has a slight effect on the deformation of the pneumatic spring at different speeds of the high-speed rolling stock.

It was established that in the range of rolling stock speeds of 170–250 km/h, the diameter of the connecting pipeline is 30 mm, and the volume of the additional tank is from 30 to 60 l, the maximum change in the dynamic stiffness of the pneumatic spring up to 15.5 % occurs at the pressure in the spring of 6.5 bar.

Dependences of energy loss and damping coefficient during the operating cycle of the pneumatic spring suspension system were derived. It was established that an increase in the volume of the additional tank and the initial pressure in the pneumatic spring leads to an increase in the energy loss during the operation cycle of the pneumatic system. The maximum values of the damping coefficient over the entire considered range of variable parameters are 1.16–1.29.

It was established that with the volume of the additional tank in the range from 30 to 50 liters, the maximum values of the damping coefficient are observed at a diameter of the connecting pipeline of 25 mm and a speed of movement from 200 to 250 km/h. And with an additional tank volume of 60 liters – with a diameter of 30 mm and a speed of 170 to 250 km/h

Author Biographies

Andrii Kuzyshyn, Lviv Polytechnic National University

Doctor of Philosophy

Department of Railway Transport

Vitalii Kovalchuk, Lviv Polytechnic National University

Doctor of Technical Sciences, Professor

Department of Railway Transport

Yuliya Sobolevska, Lviv Polytechnic National University

Doctor of Philosophy, Associate Professor

Department of Railway Transport

Yuriy Royko, Lviv Polytechnic National University

PhD, Associate Professor, Head of Department

Department of Transport Technologies

Ivan Kravets, Lviv Polytechnic National University

PhD

Department of Railway Transport

References

  1. Kuzyshyn, A., Sobolevska, J., Kostritsa, S., Batig, A., Boiarko, V. (2023). Mathematical modeling of the second stage of spring suspension of high-speed rolling stock. AIP Conference Proceedings. https://doi.org/10.1063/5.0120402
  2. Mendia-Garcia, I., Gil-Negrete Laborda, N., Pradera-Mallabiabarrena, A., Berg, M. (2020). A survey on the modelling of air springs – secondary suspension in railway vehicles. Vehicle System Dynamics, 60 (3), 835–864. https://doi.org/10.1080/00423114.2020.1838566
  3. Kovalchuk, V., Kuzyshyn, A., Kostritsya, S., Sobolevska, Y., Batig, A., Dovganyuk, S. (2018). Improving a methodology of theoretical determination of the frame and directing forсes in modern diesel trains. Eastern-European Journal of Enterprise Technologies, 6 (7 (96)), 19–26. https://doi.org/10.15587/1729-4061.2018.149838
  4. Kuzyshyn, A., Kostritsa, S., Ursulyak, L., Batig, A., Sobolevska, J., Voznyak, O. (2019). Research of the impact of geometric unevenness of the railway track on the dynamic parameters of the railway rolling stock with two-stage spring suspension. IOP Conference Series: Materials Science and Engineering, 664 (1), 012024. https://doi.org/10.1088/1757-899x/664/1/012024
  5. Mendia-Garcia, I., Gil-Negrete, N., Nieto, F. J., Facchinetti, A., Bruni, S. (2022). Analysis of the axial and transversal stiffness of an air spring suspension of a railway vehicle: mathematical modelling and experiments. International Journal of Rail Transportation, 12 (1), 56–75. https://doi.org/10.1080/23248378.2022.2136276
  6. Kuzyshyn, A., Batig, A., Kostritsa, S., Sobolevska, J., Kovalchuk, V., Dovhanyuk, S., Voznyak, O. (2018). Research of safety indicators of diesel train movement with two-stage spring suspension. MATEC Web of Conferences, 234, 05003. https://doi.org/10.1051/matecconf/201823405003
  7. Kuzyshyn, A., Batig, A., Kostritsa, S., Sobolevska, J., Dovhaniuk, S., Dzhus, V. (2020). Study of the dynamic behavior of rolling stock using a computer experiment. IOP Conference Series: Materials Science and Engineering, 985 (1), 012002. https://doi.org/10.1088/1757-899x/985/1/012002
  8. Oda, N., Nishimura, S. (1970). Vibration of Air Suspension Bogies and Their Design. Bulletin of JSME, 13 (55), 43–50. https://doi.org/10.1299/jsme1958.13.43
  9. Presthus, M. (2002). Derivation of air spring model parameters for train simulation. Derby (UK): Lulea University of Technology. Available at: https://www.diva-portal.org/smash/get/diva2:1023208/FULLTEXT01.pdf
  10. Eickhoff, B. M., Evans, J. R., Minnis, A. J. (1995). A Review of Modelling Methods for Railway Vehicle Suspension Components. Vehicle System Dynamics, 24 (6-7), 469–496. https://doi.org/10.1080/00423119508969105
  11. Berg, M. (1999). A Three–Dimensional Airspring Model with Friction and Orifice Damping. Vehicle System Dynamics, 33 (sup1), 528–539. https://doi.org/10.1080/00423114.1999.12063109
  12. Bruni, S., Vinolas, J., Berg, M., Polach, O., Stichel, S. (2011). Modelling of suspension components in a rail vehicle dynamics context. Vehicle System Dynamics, 49 (7), 1021–1072. https://doi.org/10.1080/00423114.2011.586430
  13. Quaglia, G., Sorli, M. (2001). Air Suspension Dimensionless Analysis and Design Procedure. Vehicle System Dynamics, 35 (6), 443–475. https://doi.org/10.1076/vesd.35.6.443.2040
  14. Nieto, A. J., Morales, A. L., González, A., Chicharro, J. M., Pintado, P. (2008). An analytical model of pneumatic suspensions based on an experimental characterization. Journal of Sound and Vibration, 313 (1-2), 290–307. https://doi.org/10.1016/j.jsv.2007.11.027
  15. Doquier, N. (2010). Multiphysics modelling of multibody systems – application to railway pneumatic suspensions. Louvain-la-Neuve: Universite Catholique de Louvain. Available at: https://dial.uclouvain.be/pr/boreal/object/boreal:33474/datastream/PDF_01/view
  16. Docquier, N., Fisette, P., Jeanmart, H. (2007). Multiphysic modelling of railway vehicles equipped with pneumatic suspensions. Vehicle System Dynamics, 45 (6), 505–524. https://doi.org/10.1080/00423110601050848
  17. Facchinetti, A., Mazzola, L., Alfi, S., Bruni, S. (2010). Mathematical modelling of the secondary airspring suspension in railway vehicles and its effect on safety and ride comfort. Vehicle System Dynamics, 48 (sup1), 429–449. https://doi.org/10.1080/00423114.2010.486036
  18. Kuzyshyn, A., Kovalchuk, V., Stankevych, V., Hilevych, V. (2023). Determining patterns in the influence of the geometrical parameters of the connecting pipeline on the dynamic parameters of the pneumatic spring of railroad rolling stock. Eastern-European Journal of Enterprise Technologies, 1 (7 (121)), 57–65. https://doi.org/10.15587/1729-4061.2023.274180
  19. Reidemeister, O. H., Kivisheva, A. V. (2016). Dependence of air spring parameters on throttle resistance. Science and Transport Progress, 2 (62), 157–164. https://doi.org/10.15802/stp2016/67339
  20. Xu, L. (2020). Mathematical Modeling and Characteristic Analysis of the Vertical Stiffness for Railway Vehicle Air Spring System. Mathematical Problems in Engineering, 2020, 1–12. https://doi.org/10.1155/2020/2036563
  21. Li, X., Li, T. (2013). Research on vertical stiffness of belted air springs. Vehicle System Dynamics, 51 (11), 1655–1673. https://doi.org/10.1080/00423114.2013.819984
  22. Zhu, H., Yang, J., Zhang, Y., Feng, X. (2017). A novel air spring dynamic model with pneumatic thermodynamics, effective friction and viscoelastic damping. Journal of Sound and Vibration, 408, 87–104. https://doi.org/10.1016/j.jsv.2017.07.015
  23. Li, X., Wei, Y., He, Y. (2016). Simulation on polytropic process of air springs. Engineering Computations, 33 (7), 1957–1968. https://doi.org/10.1108/ec-08-2015-0224
  24. Sayyaadi, H., Shokouhi, N. (2010). Effects of air reservoir volume and connecting pipes' length and diameter on the air spring behavior inrail–vehicles. Iranian Journal of Science & Technology, Transaction B: Engineering, 34 (B5), 499–508. Available at: https://ijstm.shirazu.ac.ir/article_916_157948bcc403bde6684123802e17f1d1.pdf
  25. Mendia-Garcia, I., Facchinetti, A., Bruni, S., Gil-Negrete, N. (2023). Analysis and modelling of the dynamic stiffness up to 400 Hz of an air spring with a pipeline connected to a reservoir. Journal of Sound and Vibration, 557, 117740. https://doi.org/10.1016/j.jsv.2023.117740
  26. Zheng, Y., Shangguan, W.-B. (2023). A combined analytical model for orifice-type and pipe-type air springs with auxiliary chambers in dynamic characteristic prediction. Mechanical Systems and Signal Processing, 185, 109830. https://doi.org/10.1016/j.ymssp.2022.109830
  27. Mazzola, L., Berg, M. (2012). Secondary suspension of railway vehicles - air spring modelling: Performance and critical issues. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 228 (3), 225–241. https://doi.org/10.1177/0954409712470641
  28. Sayyaadi, H, Shokouhi, N. (2009). Improvement of passengers ride comfort in rail vehicles equipped with air springs. World Academy of Science, Engineering and Technology, 53, 827–833. Available at: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=519a6631377f3334f9e80d6b02df0ab15b87c024
  29. Sysyn, M., Nabochenko, O., Kovalchuk, V., Gerber, U. (2019). Evaluation of railway ballast layer consolidation after maintenance works. Acta Polytechnica, 59 (1), 77–87. https://doi.org/10.14311/ap.2019.59.0077
  30. Sysyn, M., Nabochenko, O., Kovalchuk, V., Gruen, D., Pentsak, A. (2019). Improvement of inspection system for common crossings by track side monitoring and prognostics. Structural Monitoring and Maintenance, 6 (3), 219–235. Available at: https://crust.ust.edu.ua/items/70644a7f-f72e-4b9f-a36a-b367115d3bd3
  31. Przybylowicz, M., Sysyn, M., Kovalchuk, V., Nabochenko, O., Parneta, B. (2020). Experimental and theoretical evaluation of side tamping method for ballasted railway track maintenance. Transport Problems, 15 (3), 93–106. https://doi.org/10.21307/tp-2020-036
  32. Sysyn, M., Gerber, U., Gruen, D., Nabochenko, O., Kovalchuk, V. (2019). Modelling and vehicle based measurements of ballast settlements under the common crossing. European Transport - Trasporti Europei, 71. Available at: https://www.researchgate.net/publication/332712273_Modelling_and_vehicle_based_measurements_of_ballast_settlements_under_the_common_crossing
  33. Sysyn, M., Kovalchuk, V., Gerber, U., Nabochenko, O., Parneta, B. (2019). Laboratory Evaluation of Railway Ballast Consolidation by the Non-Destructive Testing. Communications - Scientific Letters of the University of Zilina, 21 (2), 81–88. https://doi.org/10.26552/com.c.2019.2.81-88
Determining the effect of additional tank volume and air pressure in the spring on the dynamic indicators of a pneumatic system of spring suspension in high-speed railroad rolling stock

Downloads

Published

2024-06-28

How to Cite

Kuzyshyn, A., Kovalchuk, V., Sobolevska, Y., Royko, Y., & Kravets, I. (2024). Determining the effect of additional tank volume and air pressure in the spring on the dynamic indicators of a pneumatic system of spring suspension in high-speed railroad rolling stock. Eastern-European Journal of Enterprise Technologies, 3(7 (129), 47–62. https://doi.org/10.15587/1729-4061.2024.304051

Issue

Vol. 3 No. 7 (129) (2024): Applied mechanics

Section

Applied mechanics

License

Copyright (c) 2024 Andrii Kuzyshyn, Vitalii Kovalchuk, Yuliya Sobolevska, Yuriy Royko, Vitaliy Korendiy, Ivan Kravets

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.