Construction of a mathematical model of an impact device with a two-element striker

Authors

DOI:

https://doi.org/10.15587/1729-4061.2025.322728

Keywords:

impact device, impact prolongation, co-impact force, discrete-continuous model, boundary value problem

Abstract

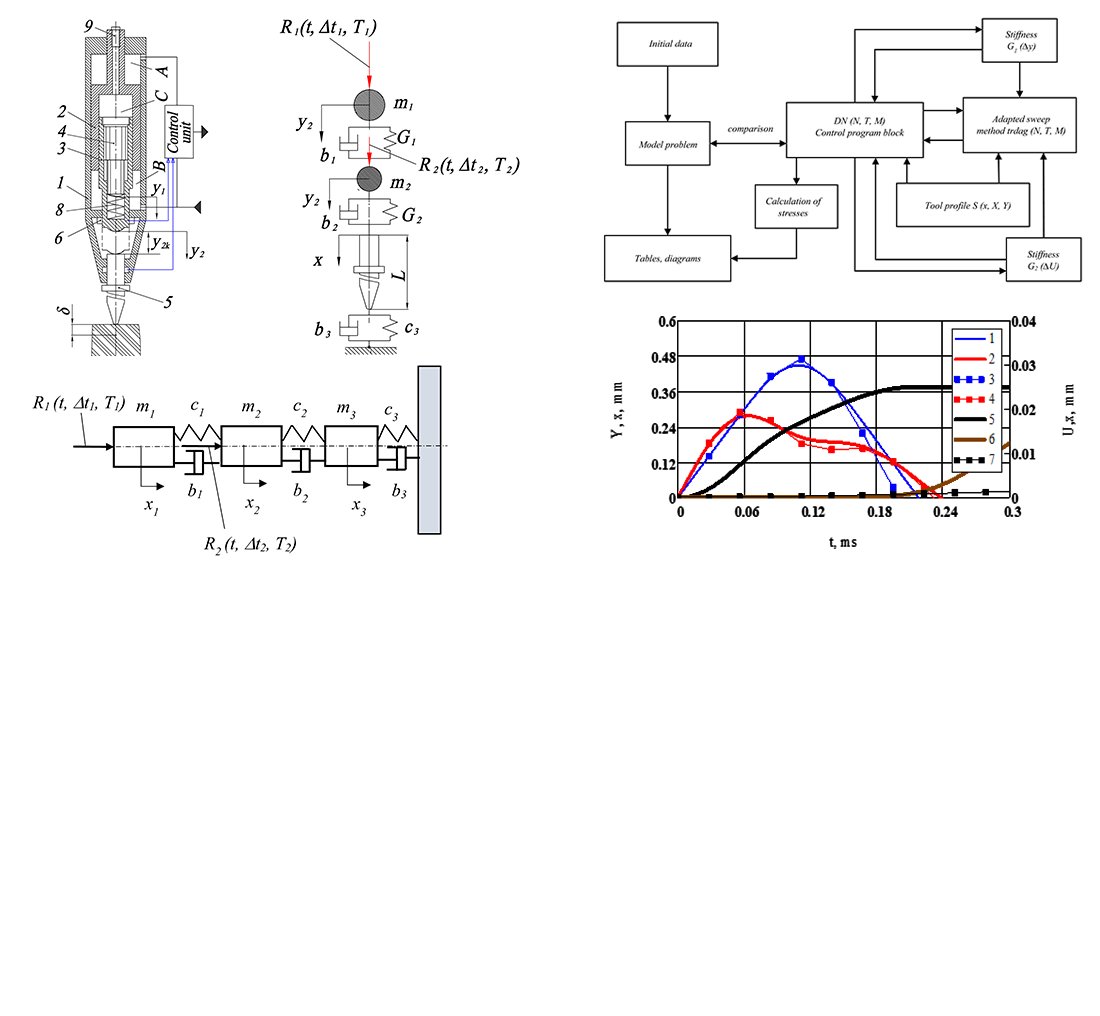
The object of this study is the oscillation process of an impact device with a two-element striker, which makes it possible to increase the efficiency of rock destruction and reduce the recoil on the device body. The task addressed was the construction of a mathematical model that describes the dynamic interaction between the striker elements and the tool while taking into account the resistance of the working medium and impulse loads on the device elements. In the given model, the tool is represented by a rod of variable cross-section, and the striker is represented by two discrete elements with reduced masses. The impact interaction is modeled by the presence of rigid and dissipative links and is described by a system of differential equations with initial and boundary conditions. To solve the initial boundary value problem, a numerical method has been used; the parameters of the method are determined by solving the model problem, which is constructed for a discrete model with three discrete masses. An increase in the co-impact time relative to a device with a solid striker by 1.5...2 times to values of 350...500 μs was established. With a load force of 50 to 500 kN in the time range of 0...1 ms and element speeds of 1...8 m/s, the normal stresses in the tool cross-sections were 200...380 MPa. The combination of discrete and continuous elements in the model made it possible to refine the numerical method, taking into account the essential properties inherent in the impulse interaction of the striker elements with the tool and the transfer of impact energy to the processing environment. The model built can be used in the design of impactors with optimal parameters for assessing the shape and duration of the shock pulse, in mining, construction, and oil production

Author Biographies

Viktor Slidenko, National Technical University of Ukraine “Igor Sikorsky Kyiv Polytechnic Institute”

Doctor of Technical Sciences, Professor

Department of Automation of Electrical and Mechatronic Complexes

Oleksandr Slidenko, “Kyiv Consulting Group” Limited Liability Company

PhD

Leonid Listovschik, National Technical University of Ukraine “Igor Sikorsky Kyiv Polytechnic Institute”

PhD, Associate Professor

Department of Automation of Electrical and Mechatronic Complexes

Anton Novykov, National Technical University of Ukraine “Igor Sikorsky Kyiv Polytechnic Institute”

PhD Student

Department of Automation of Electrical and Mechatronic Complexes

Viacheslav But, National Technical University of Ukraine “Igor Sikorsky Kyiv Polytechnic Institute”

PhD Student

Department of Automation of Electrical and Mechatronic Complexes

References

  1. Batako, A. D., Babitsky, V. I., Halliwell, N. A. (2004). Modelling of vibro-impact penetration of self-exciting percussive-rotary drill bit. Journal of Sound and Vibration, 271 (1-2), 209–225. https://doi.org/10.1016/s0022-460x(03)00642-4
  2. Batako, A. D., Babitsky, V. I., Halliwell, N. A. (2003). A self-excited system for percussive-rotary drilling. Journal of Sound and Vibration, 259 (1), 97–118. https://doi.org/10.1006/jsvi.2002.5158
  3. Neyman, V. Yu., Markov, A. V. (2018). Linear electromagnetic drive of impact machines with retaining striker. IOP Conference Series: Earth and Environmental Science, 194, 062023. https://doi.org/10.1088/1755-1315/194/6/062023
  4. Yang, G., Fang, J. (2012). Structure Parameters Optimization Analysis of Hydraulic Hammer System. Modern Mechanical Engineering, 02 (04), 137–142. https://doi.org/10.4236/mme.2012.24018
  5. Slidenko, V. M., Shevchuk, S. P., Zamaraieva, O. V., Listovshchyk, L. K. (2013). Adaptyvne funktsionuvannia impulsnykh vykonavchykh orhaniv hirnychykh mashyn. Kyiv: NTUU «KPI», 180.
  6. Zhukov, I. A., Molchanov, V. V. (2014). Rational Designing Two-Stage Anvil Block of Impact Mechanisms. Advanced Materials Research, 1040, 699–702. https://doi.org/10.4028/www.scientific.net/amr.1040.699
  7. Zhukov, I. A., Dvornikov, L. T., Nikitenko, S. M. (2016). About creation of machines for rock destruction with formation of apertures of various cross-sections. IOP Conference Series: Materials Science and Engineering, 124, 012171. https://doi.org/10.1088/1757-899x/124/1/012171
  8. Zhukov, I., Repin, A., Timofeev, E. (2018). Automated calculation and analysis of impacts generated in mining machine by anvil blocks of complex geometry. IOP Conference Series: Earth and Environmental Science, 134, 012071. https://doi.org/10.1088/1755-1315/134/1/012071
  9. Slidenko, A. M., Slidenko, V. M., Valyukhov, S. G. (2021). Discrete-continuous three-element model of impact device. Journal of Physics: Conference Series, 2131 (3), 032091. https://doi.org/10.1088/1742-6596/2131/3/032091
  10. Slidenko, V., Slidenko, O., Marchuk, L., But, V. (2023). Development of a discreet-continuous mathematical model of a percussion device with parameters of influence on the characteristics of an impact pulse. Eastern-European Journal of Enterprise Technologies, 5 (7 (125)), 70–79. https://doi.org/10.15587/1729-4061.2023.290029
  11. Vasylenko, M. V., Aleksiichuk, O. M. (2004). Teoriya kolyvan i stiykosti rukhu. Kyiv: Vyshcha shkola, 525.
  12. Samarskii, A. A. (2001). The Theory of Difference Schemes. CRC Press. https://doi.org/10.1201/9780203908518
Construction of a mathematical model of an impact device with a two-element striker

Downloads

Published

2025-02-26

How to Cite

Slidenko, V., Slidenko, O., Listovschik, L., Novykov, A., & But, V. (2025). Construction of a mathematical model of an impact device with a two-element striker . Eastern-European Journal of Enterprise Technologies, 1(7 (133), 38–49. https://doi.org/10.15587/1729-4061.2025.322728

Issue

Vol. 1 No. 7 (133) (2025): Applied mechanics

Section

Applied mechanics

License

Copyright (c) 2025 Viktor Slidenko, Oleksandr Slidenko, Leonid Listovschik, Anton Novykov, Viacheslav But

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.