Identifying the efficiency of applying of finite automata in encryption and decryption

Authors

DOI:

https://doi.org/10.15587/1729-4061.2025.331044

Keywords:

finite automata, mealy automata, cryptography with finite automata, automata composition, statistical cryptanalysis

Abstract

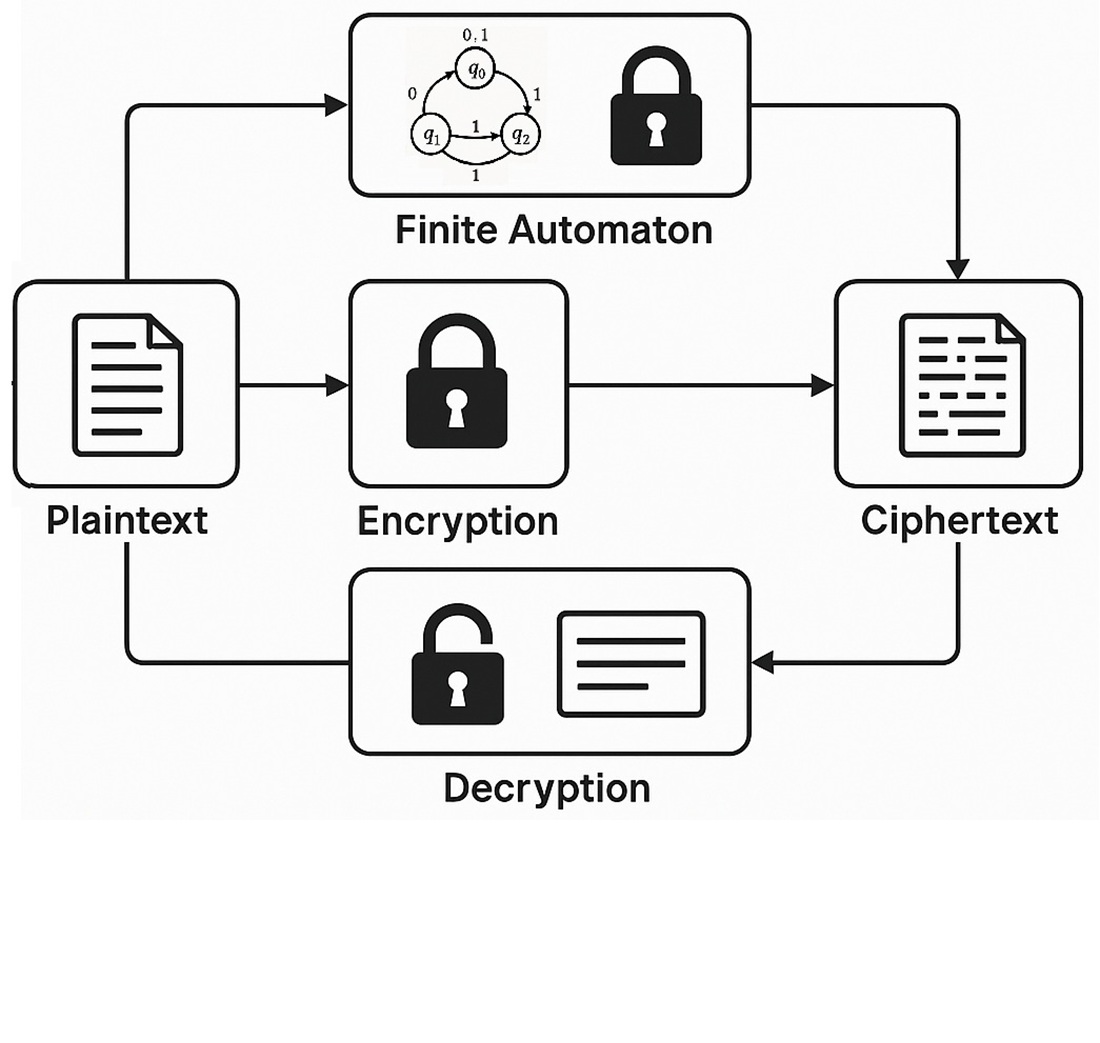
The contemporary cryptographic field is marked by efforts to enhance traditional methods through the integration of novel mathematical concepts. This fusion seeks to address the shortcomings of classical cryptography, tackle emerging security challenges, and devise more sophisticated data protection systems. Among these innovations is the application of finite automata, or CryptoAutomata, used as encoders and decoders. The object of this research is the use of finite automata, specifically CryptoAutomata, in cryptographic systems. The study addresses the problem of vulnerabilities in classical cryptographic methods, which include susceptibility to emerging cryptanalytic attacks and inefficiencies in computational overhead.

The essence of the obtained results lies in demonstrating the practical implementation and cryptographic advantages of reversible finite automata, including surjective and Mealy automata, integrated into encryption systems. Due to the inherent properties of these automata, such as reversibility, composability, and computational efficiency, the authors were able to increase the security of encryption, significantly complicating cryptanalysis attempts. These results are primarily explained by the compositional approach, which involves combining multiple finite automata to form complex encryption structures. Rigorous statistical evaluations were carried out, including NPCR and UACI, which yielded NPCR values ranging between 99.56% to 99.61% and UACI values around 33%, affirming strong resistance to differential attacks. Additionally, noise resilience was confirmed through PSNR evaluations, achieving values above 35 dB even under significant noise conditions, thereby validating robustness in practical scenarios. Furthermore, the cryptographic strength was substantiated by NIST statistical randomness tests

Author Biographies

Zhanat Saukhanova, L.N. Gumilyov Eurasian National University

Candidate of Physical and Mathematical Sciences, Associate Professor

Department of Information Security

Altynbek Sharipbay, L.N. Gumilyov Eurasian National University

Doctor of Technical Sciences, Professor

Department of Artificial Intelligence Technologies

Gulmira Shakhmetova, L.N. Gumilyov Eurasian National University

Senior Lecturer

Department of Information Security

Alibek Barlybayev, L.N. Gumilyov Eurasian National University

Doctor PhD, Professor

Department of Artificial Intelligence Technologies

Sayat Raykul, L.N. Gumilyov Eurasian National University

Student

Department of Information Security

Altay Khassenov, L.N. Gumilyov Eurasian National University

Student

Department of Information Security

References

  1. Al Busafi, S., Kumar, B. (2020). Review and Analysis of Cryptography Techniques. 2020 9th International Conference System Modeling and Advancement in Research Trends (SMART), 323–327. https://doi.org/10.1109/smart50582.2020.9336792
  2. Salami, Y., Khajevand, V., Zeinali, E. (2023). Cryptographic algorithms: a review of the literature, weaknesses and open challenges. Journal of Computer & Robotics, 16 (2). https://doi.org/10.22094/JCR.2023.1983496.1298
  3. Sharipbay, A., Saukhanova, Z., Shakhmetova, G., Barlybayev, A. (2023). Development of Reliable and Effective Methods of Cryptographic Protection of Information Based on the Finite Automata Theory. The Eurasia Proceedings of Science Technology Engineering and Mathematics, 26, 19–25. https://doi.org/10.55549/epstem.1409285
  4. Kohavi, Z., Jha, N. K. (2009). Switching and Finite Automata Theory. Cambridge University Press. https://doi.org/10.1017/cbo9780511816239
  5. Lotfi, Z., Khalifi, H., Ouardi, F. (2023). Efficient Algebraic Method for Testing the Invertibility of Finite State Machines. Computation, 11 (7), 125. https://doi.org/10.3390/computation11070125
  6. Tao, R., Chen, Sh. (1985). A finite automaton public key cryptosystem and digital signatures. Chinese Journal of Computers, 8 (6), 401–409.
  7. Abubaker, S., Wu, K. (2013). DAFA - A Lightweight DES Augmented Finite Automaton Cryptosystem. Security and Privacy in Communication Networks, 1–18. https://doi.org/10.1007/978-3-642-36883-7_1
  8. Kodada, B. (2022). FSAaCIT: Finite State Automata based One-Key Cryptosystem and Chunk-based Indexing Technique for Secure Data De-duplication in Cloud Computing. https://doi.org/10.36227/techrxiv.20443653.v1
  9. Salas Pena, P. I., Ernesto Gonzalez Torres, R. (2016). Authenticated Encryption based on finite automata cryptosystems. 2016 13th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE), 1–6. https://doi.org/10.1109/iceee.2016.7751254
  10. Gysin, M. (1996). A one-key cryptosystem based on a finite nonlinear automaton. Cryptography: Policy and Algorithms, 165–173. https://doi.org/10.1007/bfb0032356
  11. Lakshmi, S. (2012). On finite state machines and recursive functions – applications to cryptosystems. Jawaharlal Nehru Technological University.
  12. Meskanen, T. (2001). On finite automaton public key cryptosystems. TUCS Technical Report.
  13. Tao, R., Chen, S., Chen, X. (1997). FAPKC3: A new finite automaton public key cryptosystem. Journal of Computer Science and Technology, 12 (4), 289–305. https://doi.org/10.1007/bf02943149
  14. Tao, R., Chen, S. (1999). The generalization of public key cryptosystem FAPKC4. Chinese Science Bulletin, 44 (9), 784–790. https://doi.org/10.1007/bf02885019
  15. Kodada, B. B., D’Mello, D. A. (2021). Symmetric Key Cryptosystem based on Sequential State Machine. IOP Conference Series: Materials Science and Engineering, 1187 (1), 012026. https://doi.org/10.1088/1757-899x/1187/1/012026
  16. Shakhmetova, G., Barlybayev, A., Saukhanova, Z., Sharipbay, A., Raykul, S., Khassenov, A. (2024). Enhancing Visual Data Security: A Novel FSM-Based Image Encryption and Decryption Methodology. Applied Sciences, 14 (11), 4341. https://doi.org/10.3390/app14114341
  17. Zhang, M., Dong, S., Kong, H., Liu, X., Guan, H. (2016). Modeling and Simulation Strategies of Cryptographic Protocols Based on Finite State Machine. Information Technology and Intelligent Transportation Systems, 541–551. https://doi.org/10.1007/978-3-319-38789-5_62
  18. Attari, S., Shahmirzadi, A. R., Salmasizadeh, M., Gholampour, I. (2017). Finite State Machine Based Countermeasure for Cryptographic Algorithms. 2017 14th International ISC (Iranian Society of Cryptology) Conference on Information Security and Cryptology (ISCISC), 58–63. https://doi.org/10.1109/iscisc.2017.8488336
  19. Papanastasiou, P., Ottaviani, C., Pirandola, S. (2017). Finite-size analysis of measurement-device-independent quantum cryptography with continuous variables. Physical Review A, 96 (4). https://doi.org/10.1103/physreva.96.042332
  20. de la Cruz Jiménez, R. A. (2019). Generation of 8-Bit S-Boxes Having Almost Optimal Cryptographic Properties Using Smaller 4-Bit S-Boxes and Finite Field Multiplication. Progress in Cryptology – LATINCRYPT 2017, 191–206. https://doi.org/10.1007/978-3-030-25283-0_11
  21. Waseem, H. M., Khan, M. (2018). Information Confidentiality Using Quantum Spinning, Rotation and Finite State Machine. International Journal of Theoretical Physics, 57 (11), 3584–3594. https://doi.org/10.1007/s10773-018-3872-6
  22. Agrawal, S., Ishai, Y., Kushilevitz, E., Narayanan, V., Prabhakaran, M., Prabhakaran, V., Rosen, A. (2020). Cryptography from One-Way Communication: On Completeness of Finite Channels. Advances in Cryptology – ASIACRYPT 2020, 653–685. https://doi.org/10.1007/978-3-030-64840-4_22
  23. Cintas-Canto, A., Kermani, M. M., Azarderakhsh, R. (2023). Reliable Architectures for Finite Field Multipliers Using Cyclic Codes on FPGA Utilized in Classic and Post-Quantum Cryptography. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 31 (1), 157–161. https://doi.org/10.1109/tvlsi.2022.3224357
  24. Roy, A., Steiner, M. J. (2025). Generalized Triangular Dynamical System: An Algebraic System for Constructing Cryptographic Permutations over Finite Fields. Selected Areas in Cryptography – SAC 2024, 139–165. https://doi.org/10.1007/978-3-031-82841-6_6
  25. Lavanya, M., Sundar, K., Saravanan, S. (2025). Finite Field-Based Three-Tier Cryptography Algorithm to Secure the Images. Defence Science Journal, 75 (1).
  26. Sharipbay, A. (2016). Automata models in cryptography. KazNU Bulletin. Mathematics, Mechanics, Computer Science Series, 3 (1 (90)), 94–104.
  27. Bogachenko, N. (2007). Application of automata-theoretic models in cryptography. Mathematical Structures and Modeling, 1 (17), 112–120.
  28. Olson, R. (1970). On the invertibility of finite state machines. No. TR-EE-703.
  29. Tao, R. (2009). Finite Automata and Application to Cryptography. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-540-78257-5
  30. Shakhmetova, G., Saukhanova, Z., Udzir, N. I., Sharipbay, A., Saukhanov, N. (2021). Application of Pseudo-Memory Finite Automata for Information Encryption. Proceedings of the 2nd International Workshop on Intelligent Information Technologies & Systems of Information Security with CEUR-WS.
  31. Noura, H. N., Chehab, A., Couturier, R. (2020). Overview of Efficient Symmetric Cryptography: Dynamic vs Static Approaches. 2020 8th International Symposium on Digital Forensics and Security (ISDFS), 1–6. https://doi.org/10.1109/isdfs49300.2020.9116441
  32. Shakhmetova, G., Saukhanova, Z., Sharipbay, A., Ulyukova G. (2020). Using Reversible Finite-State Machines In Asymmetrical Cryptosystems. Journal of Almaty University Of Power Engineering And Communications, 1, 118.
  33. Abed, Q. K., Al-Jawher, W. A. M. (2024). Enhanced Hyperchaotic Image Encryption with CAW Transform and Sea-Lion Optimizer. Journal of Cyber Security and Mobility, 13 (5), 1207–1238. https://doi.org/10.13052/jcsm2245-1439.13517
  34. Setiadi, D. R. I. M., Rijati, N. (2023). An Image Encryption Scheme Combining 2D Cascaded Logistic Map and Permutation-Substitution Operations. Computation, 11 (9), 178. https://doi.org/10.3390/computation11090178
  35. Abusham, E., Ibrahim, B., Zia, K., Rehman, M. (2023). Facial Image Encryption for Secure Face Recognition System. Electronics, 12 (3), 774. https://doi.org/10.3390/electronics12030774
  36. Khan, S., Peng, H. (2024). A secure and adaptive block-based image encryption: a novel high-speed approach. Nonlinear Dynamics, 112 (18), 16445–16473. https://doi.org/10.1007/s11071-024-09870-8
  37. Pareschi, F., Rovatti, R., Setti, G. (2012). On Statistical Tests for Randomness Included in the NIST SP800-22 Test Suite and Based on the Binomial Distribution. IEEE Transactions on Information Forensics and Security, 7 (2), 491–505. https://doi.org/10.1109/tifs.2012.2185227
Identifying the efficiency of applying of finite automata in encryption and decryption

Downloads

Published

2025-06-25

How to Cite

Saukhanova, Z., Sharipbay, A., Shakhmetova, G., Barlybayev, A., Raykul, S., & Khassenov, A. (2025). Identifying the efficiency of applying of finite automata in encryption and decryption. Eastern-European Journal of Enterprise Technologies, 3(9 (135), 65–78. https://doi.org/10.15587/1729-4061.2025.331044

Issue

Vol. 3 No. 9 (135) (2025): Information and controlling system

Section

Information and controlling system

License

Copyright (c) 2025 Zhanat Saukhanova, Altynbek Sharipbay, Gulmira Shakhmetova, Alibek Barlybayev, Sayat Raykul, Altay Khassenov

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.