Substantiating the optimal shape of a bimetal flywheel
DOI:
https://doi.org/10.15587/1729-4061.2024.337849Keywords:
flywheel shape optimization, specific energy, bimetal structure, finite element methodAbstract
This study’s object is the flywheel as an energy storage device. The task addressed is to devise a sequential approach to flywheel shape optimization.
The analytical basis of flywheel shape optimization has been reconstructed to reveal the source of contradictory results. It was found that the product of radius and angular velocity of rotation is a constant that depends on material properties for the ring-shaped disk flywheel. It becomes somewhat more complicated for other flywheel shapes. It is the reason for the contradictions in the flywheel shape optimization results reported by researchers.
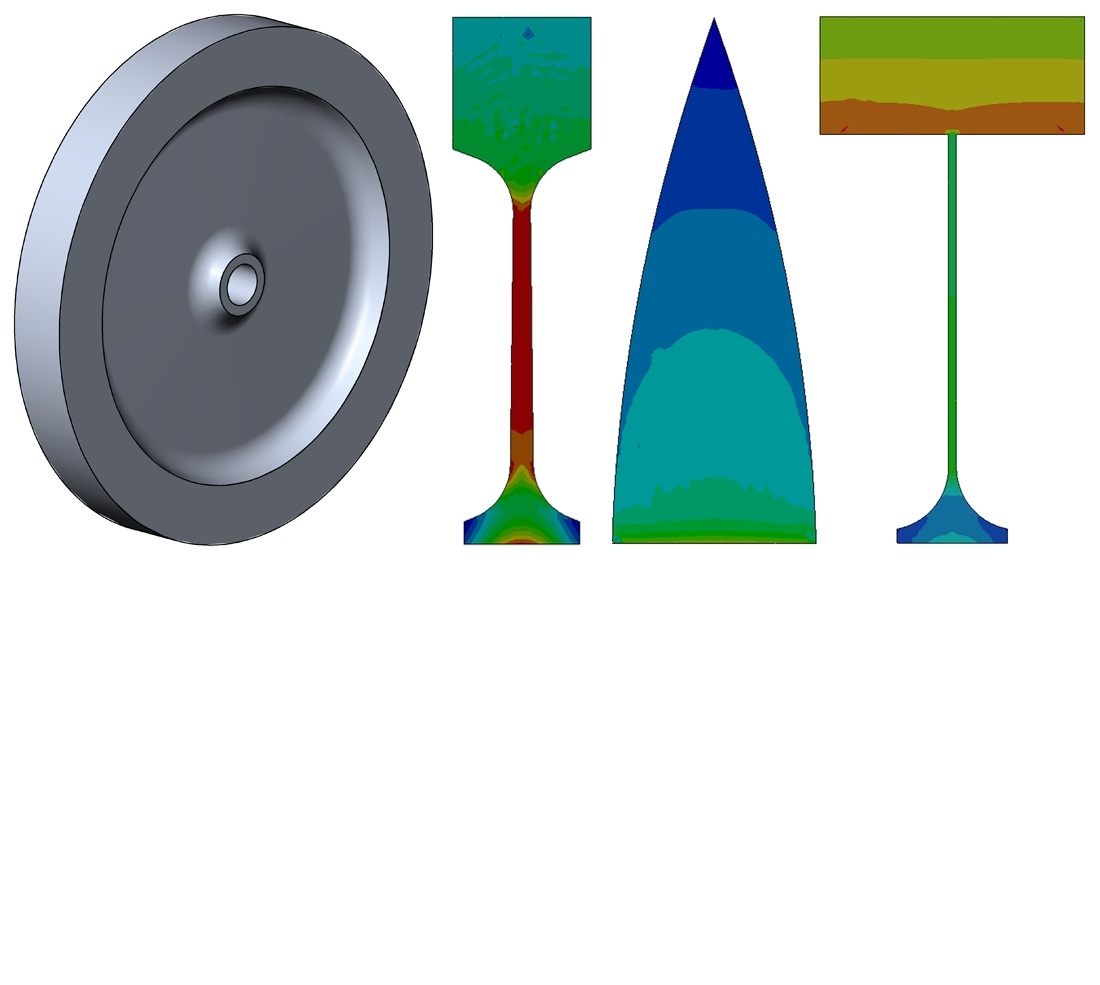
Comparative calculations for several flywheel shapes have been performed using the finite element method. The results confirmed that bringing material closer to the axis of rotation, including Laval disk shape, does not give any advantages. Material choice has an essential advantage in comparison with shape optimization. The flywheel shape has to be optimized together with the material. A ring-shaped disk flywheel is a good starting point for flywheel shape optimization. The results are attributed to the nature of the flywheel material behavior under the action of inertia forces.
A novel approach to combining different materials in flywheel construction has been proposed. One material (high-strength steel) was used for the flywheel ring. Another material with a lower elastic modulus (high-strength aluminum alloy) was used for elements connecting the ring with the shaft. The bimetal flywheel has a mass three times less than the base variant, with 24.6% underload for steel parts and 17.3% underload for aluminum parts.
The findings reported here could be practically implemented in the design and manufacturing of flywheel energy storage systems with increased specific energy for use in vehicles and stationary power units
References
- Amiryar, M., Pullen, K. (2017). A Review of Flywheel Energy Storage System Technologies and Their Applications. Applied Sciences, 7 (3), 286. https://doi.org/10.3390/app7030286
- Kale, V., Thomas, M., Secanell, M. (2021). On determining the optimal shape, speed, and size of metal flywheel rotors with maximum kinetic energy. Structural and Multidisciplinary Optimization, 64 (3), 1481–1499. https://doi.org/10.1007/s00158-021-02935-x
- Coppede, D., da Silva Bortoli, F., Moreira, J. M. L., Magalhaes, N. S., Frajuca, C. (2024). Optimization of Flywheel Rotor Energy and Stability Using Finite Element Modelling. Energies, 17 (12), 3042. https://doi.org/10.3390/en17123042
- Surwade, P. B. (2017). Design, analysis and optimization of flywheel. Spvryan’s International Journal of Engineering Sciences & Technology (SEST), 3 (4), 1–9. Available at: https://www.spvryan.org/archive/Issue3Volume4/18.pdf
- Jiang, L., Wu, C. W. (2016). Topology optimization of energy storage flywheel. Structural and Multidisciplinary Optimization, 55 (5), 1917–1925. https://doi.org/10.1007/s00158-016-1576-1
- Rufer, A. (2017). Energy Storage. CRC Press. https://doi.org/10.1201/b22265
- Singh, P., Chaudhary, H. (2018). Optimal design of the flywheel using nature inspired optimization algorithms. Open Agriculture, 3 (1), 490–499. https://doi.org/10.1515/opag-2018-0054
- Bhosale, P., Zawar, U. (2022). Shape optimization of flywheel used in agricultural thresher. arXiv. http://dx.doi.org/10.48550/arXiv.2209.02392
- Kress, G. R. (2000). Shape optimization of a flywheel. Structural and Multidisciplinary Optimization, 19 (1), 74–81. https://doi.org/10.1007/s001580050087
- Różewicz, M. (2014). Shape optimization of a flywheel. Automatyka/Automatics, 18 (1), 23. https://doi.org/10.7494/automat.2014.18.1.23
- Jaison, A. A. I., Karuppasamy, K. (2015). Design and optimization of flywheel for automobile applications. International Journal of Mechanical Engineering and Research, 5 (1), 7–13. Available at: https://www.ripublication.com/ijmer_spl/ijmaerv5n1spl_02.pdf
- Pysarenko, H. S., Kvitka, O. L., Umanskyi, E. S. (1993). Opir materialiv. Kyiv: Vyshcha shkola, 655.
- Li, X., Mittelstedt, C., Binder, A. (2022). Ein Überblick über kritische Aspekte bei der Konstruktion von Leichtbau-Schwungradrotoren mit Verbundwerkstoffen. E & i Elektrotechnik Und Informationstechnik, 139 (2), 204–221. https://doi.org/10.1007/s00502-022-01005-4
- Dems, K., Turant, J. (2009). Two approaches to the optimal design of composite flywheels. Engineering Optimization, 41 (4), 351–363. https://doi.org/10.1080/03052150802506521
- Tzeng, J., Emerson, R., Moy, P. (2006). Composite flywheels for energy storage. Composites Science and Technology, 66 (14), 2520–2527. https://doi.org/10.1016/j.compscitech.2006.01.025
- Arnold, S. M., Saleeb, A. F., Al-Zoubi, N. R. (2001). Deformation and life analysis of composite flywheel disk and multi-disk systems (NASA/TM-2001-210578). Glenn Research Center. Available at: https://ntrs.nasa.gov/api/citations/20010047395/downloads/20010047395.pdf
- Yangoz, C., Erhan, K. (2025). High-Speed Kinetic Energy Storage System Development and ANSYS Analysis of Hybrid Multi-Layered Rotor Structure. Applied Sciences, 15 (10), 5759. https://doi.org/10.3390/app15105759
- Chen, H. L., Zhu, C. S., Ye, P. (2014). A Comparison of Analysis Flywheel Stress Distributions Based on Different Material. Applied Mechanics and Materials, 536-537, 1291–1294. https://doi.org/10.4028/www.scientific.net/amm.536-537.1291
- Gulia, N. V. (2005). Superflywheels of supercarbon. The Inventor-Rationalizer, 12 (672). Available at: http://www.t-library.net/read.php?mode=image&id=6638&file=6760&page=15
- Wang, P., Gu, T., Sun, B., Liu, R., Zhang, T., Yang, J. (2022). Design and Performance Analysis of Super Highspeed Flywheel Rotor for Electric Vehicle. World Electric Vehicle Journal, 13 (8), 147. https://doi.org/10.3390/wevj13080147
- Steel and alloy guide. Available at: https://www.splav-kharkov.com/mat_start.php?name_id=170
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2025 Sergey Ryagin, Roman Onyshchenko, Volodymyr Shevchenko, Serhii Shumykin

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.








