Обґрунтування оптимальної форми біметалевого маховика

Автор(и)

  • Сергій Львович Рягін Національний університет «Запорізька політехніка», Україна https://orcid.org/0000-0002-2888-8270
  • Роман Вікторович Онищенко Національний університет «Запорізька політехніка», Україна https://orcid.org/0009-0002-3453-4089
  • Володимир Григорович Шевченко Національний університет «Запорізька політехніка», Україна https://orcid.org/0000-0001-9037-6367
  • Сергій Олександрович Шумикін Національний університет «Запорізька політехніка», Україна https://orcid.org/0000-0003-3407-2507

DOI:

https://doi.org/10.15587/1729-4061.2024.337849

Ключові слова:

оптимізація форми маховика, питома енергія, біметалева конструкція, метод скінченних елементів

Анотація

Об’єктом дослідження є маховик як пристрій для накопичення енергії. Вирішувалася проблема побудови послідовного підходу до оптимізації форми маховика.

Була реконструйована аналітична база оптимізації форми маховика для розкриття джерела суперечливості результатів. Було висвітлено, що для кільцеподібного маховика добуток радіуса та кутової швидкості обертання є константою, що залежить від властивостей матеріалу. Це стає дещо складнішим для інших форм маховиків. Це є причиною суперечливості результатів оптимізації форми маховика, що отримані дослідниками.

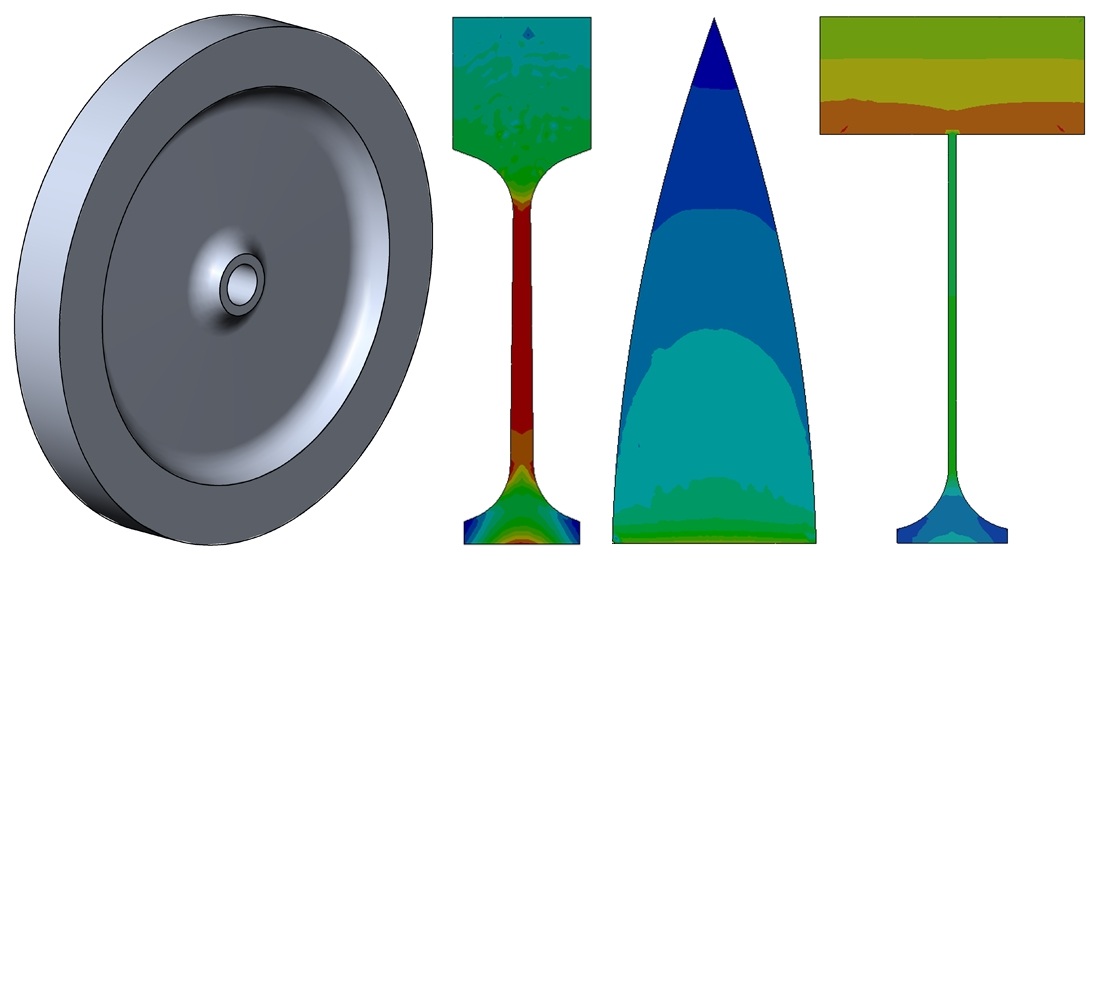
Були виконані порівняльні розрахунки з використанням методу скінченних елементів для кількох форм маховиків. Отримані результати підтвердили, що наближення матеріалу до осі обертання, включаючи форму диска Лаваля, не дає жодних переваг. Вибір матеріалу має суттєву перевагу порівняно з оптимізацією форми. Форма маховика має оптимізуватися разом з матеріалом. Кільцеподібний маховик є правильною вихідною точкою для оптимізації форми маховика. Отримані результати пояснюються природою поведінки матеріалу маховика при дії сил інерції.

Було запропоновано новий підхід до поєднання різних матеріалів у конструкції маховика. Один матеріал (високоміцна сталь) використовувався для кільця маховика. Інший матеріал з нижчим модулем пружності (високоміцний алюмінієвий сплав) використовувався для елементів, що з’єднують кільце з валом. Біметалевий маховик при рівні недовантаження 24.6% для сталевих деталей та 17.3% для алюмінієвих деталей мав масу втричі меншу порівняно з базовим варіантом.

Сферою практичного використання отриманих результатів є проєктування та виготовлення маховиків-акумуляторів з підвищеною питомою енергією для транспортних засобів та стаціонарних енергетичних установок

Біографії авторів

Сергій Львович Рягін, Національний університет «Запорізька політехніка»

Кандидат технічних наук, доцент

Кафедра теоретична та прикладна механіка

Роман Вікторович Онищенко, Національний університет «Запорізька політехніка»

Аспірант

Кафедра теоретична та прикладна механіка

Володимир Григорович Шевченко, Національний університет «Запорізька політехніка»

Кандидат технічних наук, доцент

Кафедра теоретична та прикладна механіка

Сергій Олександрович Шумикін, Національний університет «Запорізька політехніка»

Кандидат технічних наук, доцент

Кафедра теоретична та прикладна механіка

Посилання

  1. Amiryar, M., Pullen, K. (2017). A Review of Flywheel Energy Storage System Technologies and Their Applications. Applied Sciences, 7 (3), 286. https://doi.org/10.3390/app7030286
  2. Kale, V., Thomas, M., Secanell, M. (2021). On determining the optimal shape, speed, and size of metal flywheel rotors with maximum kinetic energy. Structural and Multidisciplinary Optimization, 64 (3), 1481–1499. https://doi.org/10.1007/s00158-021-02935-x
  3. Coppede, D., da Silva Bortoli, F., Moreira, J. M. L., Magalhaes, N. S., Frajuca, C. (2024). Optimization of Flywheel Rotor Energy and Stability Using Finite Element Modelling. Energies, 17 (12), 3042. https://doi.org/10.3390/en17123042
  4. Surwade, P. B. (2017). Design, analysis and optimization of flywheel. Spvryan’s International Journal of Engineering Sciences & Technology (SEST), 3 (4), 1–9. Available at: https://www.spvryan.org/archive/Issue3Volume4/18.pdf
  5. Jiang, L., Wu, C. W. (2016). Topology optimization of energy storage flywheel. Structural and Multidisciplinary Optimization, 55 (5), 1917–1925. https://doi.org/10.1007/s00158-016-1576-1
  6. Rufer, A. (2017). Energy Storage. CRC Press. https://doi.org/10.1201/b22265
  7. Singh, P., Chaudhary, H. (2018). Optimal design of the flywheel using nature inspired optimization algorithms. Open Agriculture, 3 (1), 490–499. https://doi.org/10.1515/opag-2018-0054
  8. Bhosale, P., Zawar, U. (2022). Shape optimization of flywheel used in agricultural thresher. arXiv. http://dx.doi.org/10.48550/arXiv.2209.02392
  9. Kress, G. R. (2000). Shape optimization of a flywheel. Structural and Multidisciplinary Optimization, 19 (1), 74–81. https://doi.org/10.1007/s001580050087
  10. Różewicz, M. (2014). Shape optimization of a flywheel. Automatyka/Automatics, 18 (1), 23. https://doi.org/10.7494/automat.2014.18.1.23
  11. Jaison, A. A. I., Karuppasamy, K. (2015). Design and optimization of flywheel for automobile applications. International Journal of Mechanical Engineering and Research, 5 (1), 7–13. Available at: https://www.ripublication.com/ijmer_spl/ijmaerv5n1spl_02.pdf
  12. Pysarenko, H. S., Kvitka, O. L., Umanskyi, E. S. (1993). Opir materialiv. Kyiv: Vyshcha shkola, 655.
  13. Li, X., Mittelstedt, C., Binder, A. (2022). Ein Überblick über kritische Aspekte bei der Konstruktion von Leichtbau-Schwungradrotoren mit Verbundwerkstoffen. E & i Elektrotechnik Und Informationstechnik, 139 (2), 204–221. https://doi.org/10.1007/s00502-022-01005-4
  14. Dems, K., Turant, J. (2009). Two approaches to the optimal design of composite flywheels. Engineering Optimization, 41 (4), 351–363. https://doi.org/10.1080/03052150802506521
  15. Tzeng, J., Emerson, R., Moy, P. (2006). Composite flywheels for energy storage. Composites Science and Technology, 66 (14), 2520–2527. https://doi.org/10.1016/j.compscitech.2006.01.025
  16. Arnold, S. M., Saleeb, A. F., Al-Zoubi, N. R. (2001). Deformation and life analysis of composite flywheel disk and multi-disk systems (NASA/TM-2001-210578). Glenn Research Center. Available at: https://ntrs.nasa.gov/api/citations/20010047395/downloads/20010047395.pdf
  17. Yangoz, C., Erhan, K. (2025). High-Speed Kinetic Energy Storage System Development and ANSYS Analysis of Hybrid Multi-Layered Rotor Structure. Applied Sciences, 15 (10), 5759. https://doi.org/10.3390/app15105759
  18. Chen, H. L., Zhu, C. S., Ye, P. (2014). A Comparison of Analysis Flywheel Stress Distributions Based on Different Material. Applied Mechanics and Materials, 536-537, 1291–1294. https://doi.org/10.4028/www.scientific.net/amm.536-537.1291
  19. Gulia, N. V. (2005). Superflywheels of supercarbon. The Inventor-Rationalizer, 12 (672). Available at: http://www.t-library.net/read.php?mode=image&id=6638&file=6760&page=15
  20. Wang, P., Gu, T., Sun, B., Liu, R., Zhang, T., Yang, J. (2022). Design and Performance Analysis of Super Highspeed Flywheel Rotor for Electric Vehicle. World Electric Vehicle Journal, 13 (8), 147. https://doi.org/10.3390/wevj13080147
  21. Steel and alloy guide. Available at: https://www.splav-kharkov.com/mat_start.php?name_id=170
Обґрунтування оптимальної форми біметалевого маховика

##submission.downloads##

Опубліковано

2025-08-28

Як цитувати

Рягін, С. Л., Онищенко, Р. В., Шевченко, В. Г., & Шумикін, С. О. (2025). Обґрунтування оптимальної форми біметалевого маховика. Eastern-European Journal of Enterprise Technologies, 4(7 (136), 23–31. https://doi.org/10.15587/1729-4061.2024.337849

Номер

Том 4 № 7 (136) (2025): Прикладна механіка

Розділ

Прикладна механіка

Ліцензія

Авторське право (c) 2025 Sergey Ryagin, Roman Onyshchenko, Volodymyr Shevchenko, Serhii Shumykin

Creative Commons License

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.

Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.

Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.