Designing a gravity chute based on the given trajectory of cargo movement
DOI:
https://doi.org/10.15587/1729-4061.2025.340389Keywords:
Frenet and Darboux trihedra, arc length, applied forces, differential equations, helixAbstract
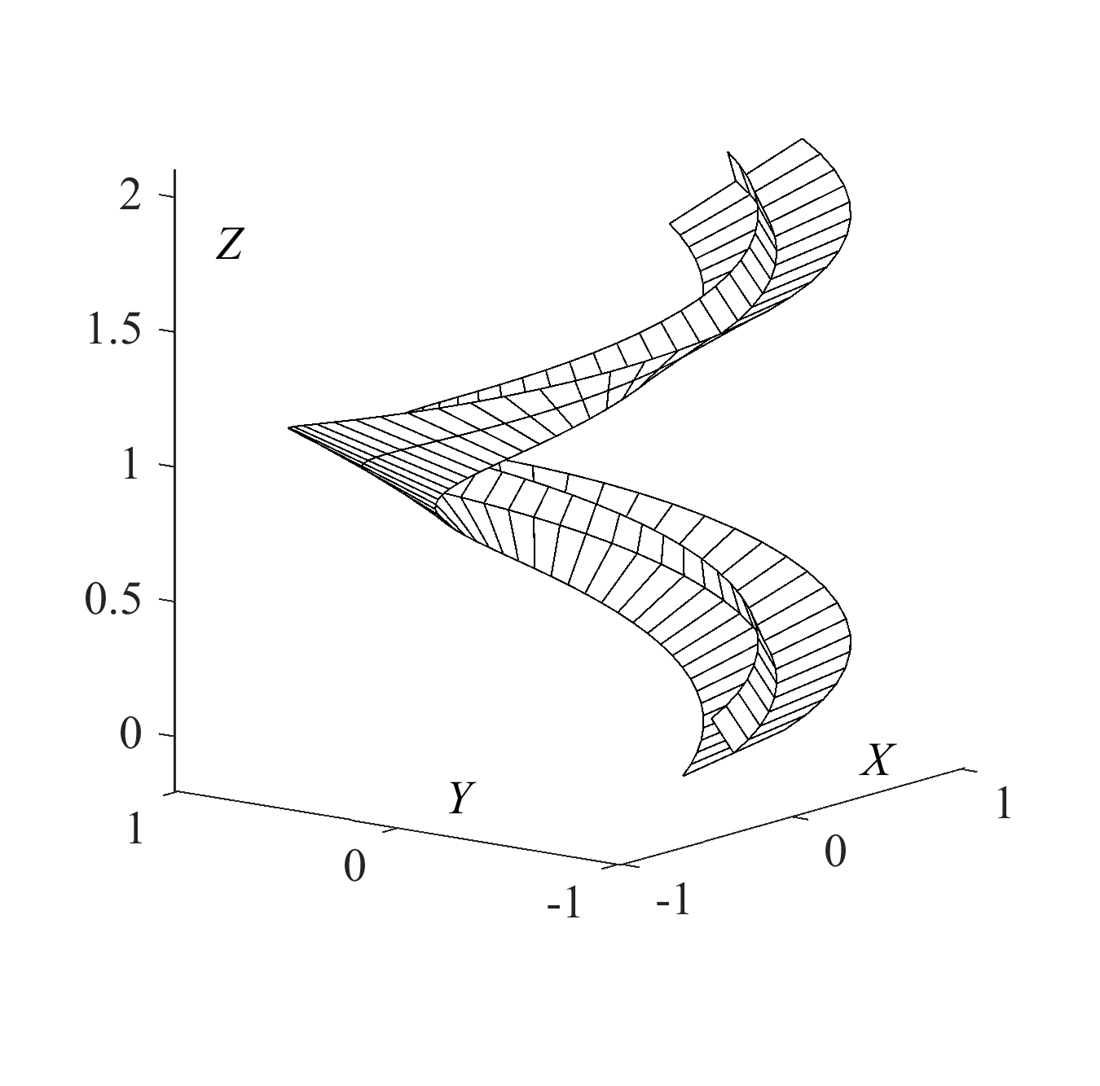
This study's object is the process of cargo movement along the helical surface of an oblique open helicoid under the action of its natural weight. Such movement takes place in gravity chutes where the cargo descends under the action of its natural weight. Gravity (screw) chutes are used for transportation, separation, and enrichment of material.
For a given surface, the problem is solved by composing differential equations of motion of a mathematical point, which is conditionally replaced by cargo, in projections onto the axis of the spatial coordinate system. If the surface is helical, then after stabilization of the motion, it is possible to find the parameters of the helical line – the trajectory of cargo movement. The task implies solving the inverse problem – constructing a helical surface along a given trajectory of cargo descent, which is a helical line.
The results are attributed to the use of two accompanying trihedra of the trajectory with a common vertex and tangent orts to the trajectory, which coincide. One of them is a Frenet trihedron whose position is determined by the differential characteristics of the curve, and the second is a Darboux trihedron, the position of which depends on the point of the trajectory on the surface. In addition to the two coincident orts, the remaining four orts are located in the plane normal to the trajectory. The use of these two orts makes it possible to compose differential equations of motion of the load in projections onto a moving Darboux trihedron, one of the planes of which is tangent to the surface.
A feature of the solution to the problem is that the trajectory of the load, i.e., the helix, is given by radius r of the cylinder on which it is located and velocity V of the load. Using these data, angle β of its ascent is determined. For example, at r = 0.5 m, V = 2.5 m/s, the angle of elevation is β = 20.7°. Then, a helical linear surface is constructed that passes through the given trajectory
References
- Trokhaniak, O. (2023). Determination of optimal parameters of hinged operating elements of screw conveyers. Machinery & Energetics, 14 (1). https://doi.org/10.31548/machinery/1.2023.79
- Trokhaniak, O. (2022). Estimation of eddy currents and power losses in the rotor of a screw electrothermomechanical converter for additive manufacturing. Machinery & Energetics, 13 (3). https://doi.org/10.31548/machenergy.13(3).2022.92-98
- Klendii, M., Logusch, I., Dragan, A., Tsvartazkii, I., Grabar, A. (2022). Justification and calculation of design and strength parameters of screw loaders. Machinery & Energetics, 13 (4). https://doi.org/10.31548/machenergy.13(4).2022.48-59
- Chvartatskiy, I., Flonts, I., Grabar, A., Shatrov, R. (2021). Synthesis of energy-saving transport-technological systems with screw working bodies. Machinery & Energetics, 12 (4). https://doi.org/10.31548/machenergy2021.04.077
- Bogomolov, O. V., Braginets, M. V., Khmelovskyi, V. S., Bogomolov, O. O. (2021). Research of gravity separator of rapesee. Machinery & Energetics, 12 (2), 77–82. https://doi.org/10.31548/machenergy2021.02.077
- Aliiev, E., Vedmedeva, K. (2025). Automated devices for quantitative phenotyping of sunflower seeds. Machinery & Energetics, 16 (1), 54–64. https://doi.org/10.31548/machinery/1.2025.54
- Nоvitskiy, A., Banniy, O., Novitskyi, Y., Antal, M. (2023). A study of mixer-feeder equipment operational reliability. Machinery & Energetics, 14 (4), 101–110. https://doi.org/10.31548/machinery/4.2023.101
- Zablodskiy, M., Kovalchuk, S., Gritsyuk, V., Subramanian, P. (2023). Screw electromechanical hydrolyzer for processing poultry by-products. Machinery & Energetics, 14 (1). https://doi.org/10.31548/machinery/1.2023.36
- Bidas, M., Galecki, G. (2021). The concept of a screw conveyor for the vertical transport of bulk materials. Mining Machines, 39, 28–33. https://doi.org/10.32056/KOMAG2021.3.3
- Moelder, K., Lillerand, T. (2025). Design and feasbility analysis of vertical static flight screw conveyor usage in granulated fertilizer transportation. 24th International Scientific Conference Engineering for Rural Development Proceedings, 24. https://doi.org/10.22616/erdev.2025.24.tf090
- Minglani, D., Sharma, A., Pandey, H., Dayal, R., Joshi, J. B., Subramaniam, S. (2020). A review of granular flow in screw feeders and conveyors. Powder Technology, 366, 369–381. https://doi.org/10.1016/j.powtec.2020.02.066
- Karwat, B., Rubacha, P., Stańczyk, E. (2020). Simulational and experimental determination of the exploitation parameters of a screw conveyor. Eksploatacja i Niezawodność – Maintenance and Reliability, 22 (4), 741–747. https://doi.org/10.17531/ein.2020.4.18
- Lian, G., Zhong, W., Liu, X. (2021). DEM study on the mixed feeding process of coal and cylindroid biomass particles in a screw feeder. Advanced Powder Technology, 32 (7), 2543–2554. https://doi.org/10.1016/j.apt.2021.05.031
- Wenwu, Y., Longyu, F., Xiwen, L., Hui, L., Yangqing, Y., Zhanhao, L. (2020). Experimental study of the effects of discharge port parameters on the fertilizing performance for fertilizer distribution apparatus with screw. Transactions of the Chinese Society of Agricultural Engineering, 36 (17), 1–8. https://dx.doi.org/10.11975/j.issn.1002-6819.2020.17.001
- Kresan, Т. (2020). Calculation of gravitation descent formed by surface of skew closed helicoid. Machinery & Energetics, 11 (2), 49–57. Available at: https://technicalscience.com.ua/en/journals/t-11-2-2020/rozrakhunok-gravitatsiynogo-spusku-utvoryenogo-povyerkhnyeyu-kosogo-zakritogo-gyelikoyida
- Xin, M., Jiang, Z., Song, Y., Cui, H., Kong, A., Chi, B., Shan, R. (2023). Compression Strength and Critical Impact Speed of Typical Fertilizer Grains. Agriculture, 13 (12), 2285. https://doi.org/10.3390/agriculture13122285
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2025 Tetiana Volina, Victor Nesvidomin, Serhii Pylypaka, Mykhailo Kalenyk, Vitalii Ploskyi, Natalia Ausheva, Vitaliy Babka, Olena Nalobina, Serhii Andrukh, Oleksandr Pavlenko

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.








