Конструювання гравітаційного спуску за заданою траєкторією руху вантажу
DOI:
https://doi.org/10.15587/1729-4061.2025.340389Ключові слова:
тригранники Френе і Дарбу, довжина дуги, прикладені сили, диференціальні рівняння, гвинтова лініяАнотація
Об’єктом дослідження є процес руху вантажу по гвинтовій поверхні косого відкритого гелікоїда під дією сили власної ваги. Такий рух має місце в гравітаційних спусках, де вантаж опускається під дією сили власної ваги. Гравітаційні (гвинтові) спуски застосовують для транспортування, сепарації і збагачення матеріалу. При заданій поверхні задача розв’язується складанням диференціальних рівнянь руху математичної точки, яку умовно замінюють вантажем, в проєкціях на осі просторової системи координат. Якщо поверхня гвинтова, то після стабілізації руху можна знайти параметри гвинтової лінії – траєкторії руху вантажу. Проблема полягає в розв’язанні оберненої задачі – конструюванні гвинтової поверхні за заданою траєкторією опускання вантажу, якою є гвинтова лінія.
Отримані результати пояснюються застосуванням двох супровідних тригранників траєкторії із спільною вершиною і дотичними ортами до траєкторії, які збігаються. Один із них є тригранником Френе, положення якого визначається диференціальними характеристиками кривої, а другий – тригранником Дарбу, положення якого залежить від точки траєкторії на поверхні. Крім двох ортів, що збігаються, решта чотири орти розташовані в нормальній до траєкторії площині. Застосування цих двох ортів дає можливість скласти диференціальні рівняння руху вантажу в проєкціях на рухомий тригранник Дарбу, одна із площин якого є дотичною до поверхні.
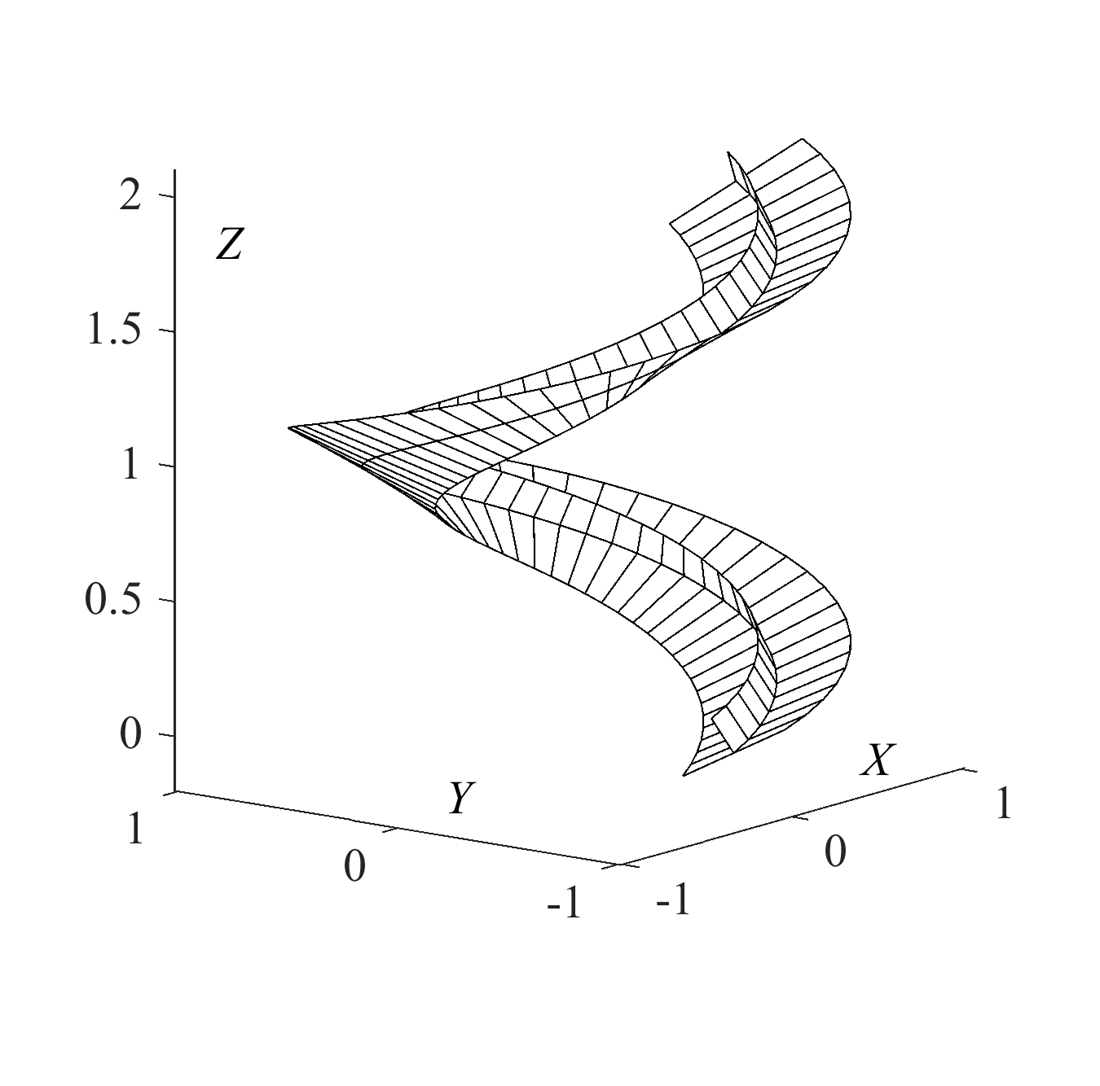
Особливістю розв’язання задачі є те, що траєкторія руху вантажу, тобто гвинтова лінія, задається радіусом r циліндра, на якому вона розташована, і швидкістю V руху вантажу. За допомогою цих даних визначається кут β її підйому. Наприклад, при r = 0,5 м, V = 2,5 м/с кут підйому становить β = 20,7°. Після цього відбувається побудова гвинтової лінійчатої поверхні, яка проходить через задану траєкторію
Посилання
- Trokhaniak, O. (2023). Determination of optimal parameters of hinged operating elements of screw conveyers. Machinery & Energetics, 14 (1). https://doi.org/10.31548/machinery/1.2023.79
- Trokhaniak, O. (2022). Estimation of eddy currents and power losses in the rotor of a screw electrothermomechanical converter for additive manufacturing. Machinery & Energetics, 13 (3). https://doi.org/10.31548/machenergy.13(3).2022.92-98
- Klendii, M., Logusch, I., Dragan, A., Tsvartazkii, I., Grabar, A. (2022). Justification and calculation of design and strength parameters of screw loaders. Machinery & Energetics, 13 (4). https://doi.org/10.31548/machenergy.13(4).2022.48-59
- Chvartatskiy, I., Flonts, I., Grabar, A., Shatrov, R. (2021). Synthesis of energy-saving transport-technological systems with screw working bodies. Machinery & Energetics, 12 (4). https://doi.org/10.31548/machenergy2021.04.077
- Bogomolov, O. V., Braginets, M. V., Khmelovskyi, V. S., Bogomolov, O. O. (2021). Research of gravity separator of rapesee. Machinery & Energetics, 12 (2), 77–82. https://doi.org/10.31548/machenergy2021.02.077
- Aliiev, E., Vedmedeva, K. (2025). Automated devices for quantitative phenotyping of sunflower seeds. Machinery & Energetics, 16 (1), 54–64. https://doi.org/10.31548/machinery/1.2025.54
- Nоvitskiy, A., Banniy, O., Novitskyi, Y., Antal, M. (2023). A study of mixer-feeder equipment operational reliability. Machinery & Energetics, 14 (4), 101–110. https://doi.org/10.31548/machinery/4.2023.101
- Zablodskiy, M., Kovalchuk, S., Gritsyuk, V., Subramanian, P. (2023). Screw electromechanical hydrolyzer for processing poultry by-products. Machinery & Energetics, 14 (1). https://doi.org/10.31548/machinery/1.2023.36
- Bidas, M., Galecki, G. (2021). The concept of a screw conveyor for the vertical transport of bulk materials. Mining Machines, 39, 28–33. https://doi.org/10.32056/KOMAG2021.3.3
- Moelder, K., Lillerand, T. (2025). Design and feasbility analysis of vertical static flight screw conveyor usage in granulated fertilizer transportation. 24th International Scientific Conference Engineering for Rural Development Proceedings, 24. https://doi.org/10.22616/erdev.2025.24.tf090
- Minglani, D., Sharma, A., Pandey, H., Dayal, R., Joshi, J. B., Subramaniam, S. (2020). A review of granular flow in screw feeders and conveyors. Powder Technology, 366, 369–381. https://doi.org/10.1016/j.powtec.2020.02.066
- Karwat, B., Rubacha, P., Stańczyk, E. (2020). Simulational and experimental determination of the exploitation parameters of a screw conveyor. Eksploatacja i Niezawodność – Maintenance and Reliability, 22 (4), 741–747. https://doi.org/10.17531/ein.2020.4.18
- Lian, G., Zhong, W., Liu, X. (2021). DEM study on the mixed feeding process of coal and cylindroid biomass particles in a screw feeder. Advanced Powder Technology, 32 (7), 2543–2554. https://doi.org/10.1016/j.apt.2021.05.031
- Wenwu, Y., Longyu, F., Xiwen, L., Hui, L., Yangqing, Y., Zhanhao, L. (2020). Experimental study of the effects of discharge port parameters on the fertilizing performance for fertilizer distribution apparatus with screw. Transactions of the Chinese Society of Agricultural Engineering, 36 (17), 1–8. https://dx.doi.org/10.11975/j.issn.1002-6819.2020.17.001
- Kresan, Т. (2020). Calculation of gravitation descent formed by surface of skew closed helicoid. Machinery & Energetics, 11 (2), 49–57. Available at: https://technicalscience.com.ua/en/journals/t-11-2-2020/rozrakhunok-gravitatsiynogo-spusku-utvoryenogo-povyerkhnyeyu-kosogo-zakritogo-gyelikoyida
- Xin, M., Jiang, Z., Song, Y., Cui, H., Kong, A., Chi, B., Shan, R. (2023). Compression Strength and Critical Impact Speed of Typical Fertilizer Grains. Agriculture, 13 (12), 2285. https://doi.org/10.3390/agriculture13122285
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2025 Tetiana Volina, Victor Nesvidomin, Serhii Pylypaka, Mykhailo Kalenyk, Vitalii Ploskyi, Natalia Ausheva, Vitaliy Babka, Olena Nalobina, Serhii Andrukh, Oleksandr Pavlenko

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.
Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.









