Devising of a method for analysing the propagation speed of car flows in a train formation plan based on synchronisation theory in complex networks

Authors

DOI:

https://doi.org/10.15587/1729-4061.2025.341559

Keywords:

Abstract

This study investigates freight transportation process in the railroad network, which is formalized in the form of a train formation plan (TFP) as a complex dynamic system.

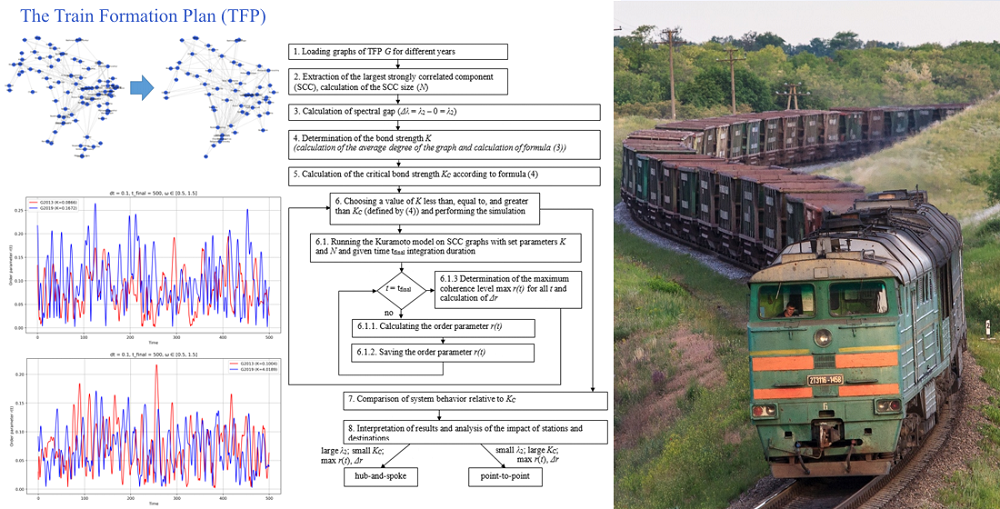
To assess the dynamic properties of a freight transportation model at the macro level of railroad system functioning, a method has been devised for analyzing the speed of transferring railroad car flows in the network. The proposed method reflects coordination dynamics not through the time of physical passage of trains in the network but through the ability of the system that organizes car flows into trains to quickly form a coherent state. The Kuramoto model was used to determine the speed of coordination. That has made it possible to distinguish TFP networks.

The application of the devised method and the simulation made it possible to compare the structural and dynamic properties of existing transportation system over the period from 2013 to 2019. The limited ability of TFP networks to global phase integration has been proven. It has been established that the TFP network in 2019 demonstrated a loss of systemic coherence, which is typical of decentralized point-to-point transportation networks. That was confirmed by calculating λ22013 ≈ 19.913342 and λ22019 ≈ 0.497646, where the difference between spectral gaps reached two orders of magnitude, while the time to reach the maximum of the order parameter rmax in 2019 was 4.07 times greater at comparable values of the order and KC = 6. This indicates the transformation of the operating model from a centralized hub-and-spoke in 2013 to a more decentralized point-to-point model in 2019.

A special feature of the results based on the study is that the proposed method makes it possible to improve the quality of macroanalysis of changes in the structural and dynamic efficiency of the TFP network.

The scope of results practical application is the railroad industry. Conditions for the practical implementation of the findings are the importance of taking into account the results when analyzing operating TFPs

Author Biographies

Andrii Kyman, Ukrainian State University of Railway Transport

PhD, Associate Professor

Department of Cargo and Commercial Work Management

Andrii Prokhorchenko, Ukrainian State University of Railway Transport

Doctor of Technical Sciences, Professor

Department of Operational Work Management

Artem Panchenko, V. N. Karazin Kharkiv National University

PhD, Associate Professor

Department of Theoretical and Applied Computer Science

Serhii Zolotarov, Ukrainian State University of Railway Transport

PhD Student

Department of Operational Work Management

Mykhailo Kravchenko, Kernel-Trade LLC

PhD

Department of Transshipment and Fleet, Logistics Division

Halyna Prokhorchenko, Ukrainian State University of Railway Transport

PhD, Associate Professor

Department of Operational Work Management

Oleksandra Orda, Kharkiv National Automobile and Highway University

PhD, Associate Professor

Department of Transport Technologies

References

  1. Strong, J. S. (2024). Operating innovation in North American railroads: Activist investors and precision scheduling railroading. Case Studies on Transport Policy, 15, 101164. https://doi.org/10.1016/j.cstp.2024.101164
  2. Butko, T., Prokhorchenko, A., Golovko, T., Prokhorchenko, G. (2018). Development of the method for modeling the propagation of delays in non­cyclic train scheduling on the railroads with mixed traffic. Eastern-European Journal of Enterprise Technologies, 1 (3 (91)), 30–39. https://doi.org/10.15587/1729-4061.2018.123141
  3. Li, B., Jiang, S., Zhou, Y., Xuan, H. (2023). Optimization of train formation plan based on technical station under railcar demand fluctuation. Journal of Industrial and Production Engineering, 40 (6), 448–463. https://doi.org/10.1080/21681015.2023.2221699
  4. Frisch, S., Hungerländer, P., Jellen, A., Lackenbucher, M., Primas, B., Steininger, S. (2022). Integrated freight car routing and train scheduling. Central European Journal of Operations Research, 31 (2), 417–443. https://doi.org/10.1007/s10100-022-00815-3
  5. Butko, T., Prokhorov, V., Chekhunov, D. (2017). Devising a method for the automated calculation of train formation plan by employing genetic algorithms. Eastern-European Journal of Enterprise Technologies, 1 (3 (85)), 55–61. https://doi.org/10.15587/1729-4061.2017.93276
  6. JSC “Ukrainian railways”. Available at: https://www.uz.gov.ua/cargo_transportation Last accessed: 12.08.2025
  7. But’ko, T., Prokhorchenko, A. (2013). Investigation into Train Flow System on Ukraine’s Railways with Methods of Complex Network Analysis. American Journal of Industrial Engineering, 1 (3), 41–45.
  8. Zhang, X., Zhu, T. (2023). Emergence of synchronization in Kuramoto model with general digraph. Discrete and Continuous Dynamical Systems – B, 28 (3), 2335–2390. https://doi.org/10.3934/dcdsb.2022172
  9. Daganzo, C. F., Geroliminis, N. (2008). An analytical approximation for the macroscopic fundamental diagram of urban traffic. Transportation Research Part B: Methodological, 42 (9), 771–781. https://doi.org/10.1016/j.trb.2008.06.008
  10. Wang, Y., Yu, X., Guo, J., Papamichail, I., Papageorgiou, M., Zhang, L. et al. (2022). Macroscopic traffic flow modelling of large-scale freeway networks with field data verification: State-of-the-art review, benchmarking framework, and case studies using METANET. Transportation Research Part C: Emerging Technologies, 145, 103904. https://doi.org/10.1016/j.trc.2022.103904
  11. de Jong, G., Vierth, I., Tavasszy, L., Ben-Akiva, M. (2012). Recent developments in national and international freight transport models within Europe. Transportation, 40 (2), 347–371. https://doi.org/10.1007/s11116-012-9422-9
  12. Butko, T., Muzykin, M., Prokhorchenko, A., Nesterenko, H., Prokhorchenko, H. (2019). Determining the Rational Motion Intensity of Train Traffic Flows on the Railway Corridors with Account for Balance of Expenses on Traction Resources and Cargo Owners. Transport and Telecommunication Journal, 20 (3), 215–228. https://doi.org/10.2478/ttj-2019-0018
  13. Szymula, C., Bešinović, N., Nachtigall, K. (2024). Quantifying periodic railway network capacity using petri nets and macroscopic fundamental diagram. Transportation Research Part C: Emerging Technologies, 158, 104436. https://doi.org/10.1016/j.trc.2023.104436
  14. Khomenko, Y., Okorokov, A., Matsiuk, V., Zhuravel, I., Pavlenko, O. (2025). Revealing the causes of delays at transit points along an intermodal grain supply chain. Eastern-European Journal of Enterprise Technologies, 4 (3 (136)), 40–50. https://doi.org/10.15587/1729-4061.2025.338166
  15. Helbing, D. (2001). Traffic and related self-driven many-particle systems. Reviews of Modern Physics, 73 (4), 1067–1141. https://doi.org/10.1103/revmodphys.73.1067
  16. Saw, V.-L., Chung, N. N., Quek, W. L., Pang, Y. E. I., Chew, L. Y. (2019). Bus bunching as a synchronisation phenomenon. Scientific Reports, 9 (1). https://doi.org/10.1038/s41598-019-43310-7
  17. Kuramoto, Y.; Araki, H. (Ed.) (1975). Lecture Notes in Physics, International Symposium on Mathematical Problems in Theoretical Physics. Vol. 39. New York: Springer-Verlag, 420.
  18. Rodriguez, M., Fathy, H. K. (2022). Distributed Kuramoto Self-Synchronization of Vehicle Speed Trajectories in Traffic Networks. IEEE Transactions on Intelligent Transportation Systems, 23 (7), 6786–6796. https://doi.org/10.1109/tits.2021.3062178
  19. Fretter, C., Krumov, L., Weihe, K., Müller-Hannemann, M., Hütt, M.-T. (2010). Phase synchronization in railway timetables. The European Physical Journal B, 77 (2), 281–289. https://doi.org/10.1140/epjb/e2010-00234-y
  20. Yoon, S., Sorbaro Sindaci, M., Goltsev, A. V., Mendes, J. F. F. (2015). Critical behavior of the relaxation rate, the susceptibility, and a pair correlation function in the Kuramoto model on scale-free networks. Physical Review E, 91 (3). https://doi.org/10.1103/physreve.91.032814
  21. Wang, Y., Doyle, F. J. (2013). Exponential Synchronization Rate of Kuramoto Oscillators in the Presence of a Pacemaker. IEEE Transactions on Automatic Control, 58 (4), 989–994. https://doi.org/10.1109/tac.2012.2215772
  22. Wang, W., Du, W., Liu, K., Tong, L. (2022). The Evolution of China’s Railway Network (CRN) 1999-2019: Urbanization Impact and Regional Connectivity. Urban Rail Transit, 8 (2), 134–145. https://doi.org/10.1007/s40864-022-00168-9
  23. Peng, S., Lu, J., Jiang, B., Zhu, J. (2024). Synchronization of high-dimensional Kuramoto-oscillator networks with variable-gain impulsive coupling on the unit sphere. Nonlinear Analysis: Hybrid Systems, 54, 101536. https://doi.org/10.1016/j.nahs.2024.101536
  24. Lei, L., Han, W., Yang, J. (2021). Kuramoto model with correlation between coupling strength and natural frequency. Chaos, Solitons & Fractals, 144, 110734. https://doi.org/10.1016/j.chaos.2021.110734
  25. Böhle, T., Kuehn, C., Thalhammer, M. (2021). On the reliable and efficient numerical integration of the Kuramoto model and related dynamical systems on graphs. International Journal of Computer Mathematics, 99 (1), 31–57. https://doi.org/10.1080/00207160.2021.1952997
  26. Gherardini, S., Gupta, S., Ruffo, S. (2018). Spontaneous synchronisation and nonequilibrium statistical mechanics of coupled phase oscillators. Contemporary Physics, 59 (3), 229–250. https://doi.org/10.1080/00107514.2018.1464100
  27. McGraw, P. N., Menzinger, M. (2007). Analysis of nonlinear synchronization dynamics of oscillator networks by Laplacian spectral methods. Physical Review E, 75 (2). https://doi.org/10.1103/physreve.75.027104
  28. O’Kelly, M. E., Park, Y. (2023). Contrasts in Sustainability between Hub-Based and Point-to-Point Airline Networks. Sustainability, 15 (20), 15111. https://doi.org/10.3390/su152015111
  29. Sabhahit, N. G., Khurd, A. S., Jalan, S. (2024). Prolonged hysteresis in the Kuramoto model with inertia and higher-order interactions. Physical Review E, 109 (2). https://doi.org/10.1103/physreve.109.024212
  30. Arenas, A., Díaz-Guilera, A., Kurths, J., Moreno, Y., Zhou, C. (2008). Synchronization in complex networks. Physics Reports, 469 (3), 93–153. https://doi.org/10.1016/j.physrep.2008.09.002
Devising of a method for analysing the propagation speed of car flows in a train formation plan based on synchronisation theory in complex networks

Downloads

Published

2025-10-31

How to Cite

Kyman, A., Prokhorchenko, A., Panchenko, A., Zolotarov, S., Kravchenko, M., Prokhorchenko, H., & Orda, O. (2025). Devising of a method for analysing the propagation speed of car flows in a train formation plan based on synchronisation theory in complex networks. Eastern-European Journal of Enterprise Technologies, 5(3 (137), 56–67. https://doi.org/10.15587/1729-4061.2025.341559

Issue

Vol. 5 No. 3 (137) (2025): Control processes

Section

Control processes

License

Copyright (c) 2025 Andrii Kyman, Andrii Prokhorchenko, Artem Panchenko, Serhii Zolotarov, Mykhailo Kravchenko, Halyna Prokhorchenko, Oleksandra Orda

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.