Розрока методу аналізу швидкості передачі вагонопотоків у плані формування поїздів на основі теорії синхронизації в складних мережах

Автор(и)

  • Андрій Миколайович Киман Український державний університет залізничного транспорту, Україна http://orcid.org/0000-0002-4000-3287
  • Андрій Володимирович Прохорченко Український державний університет залізничного транспорту, Україна http://orcid.org/0000-0003-3123-5024
  • Артем Сергійович Панченко Харківський національний університету ім. В. Н. Каразіна, Україна https://orcid.org/0000-0001-5865-6158
  • Сергій Анатолійович Золотрьов Український державний університет залізничного транспорту, Україна https://orcid.org/0009-0001-5951-4589
  • Михайло Анатолійович Кравченко ТОВ «Кернел-Трейд», Україна https://orcid.org/0000-0001-7445-8952
  • Галина Олегівна Прохорченко Український державний університет залізничного транспорту, Україна http://orcid.org/0000-0003-1158-3953
  • Олександра Олександрівна Орда Харківський національний автомобільно-дорожній університет, Україна https://orcid.org/0000-0002-7213-8469

DOI:

https://doi.org/10.15587/1729-4061.2025.341559

Ключові слова:

Rail freight, залізнична система, вагонопотік, план формування, hub-and-spoke, point-to-point, модель Курамото

Анотація

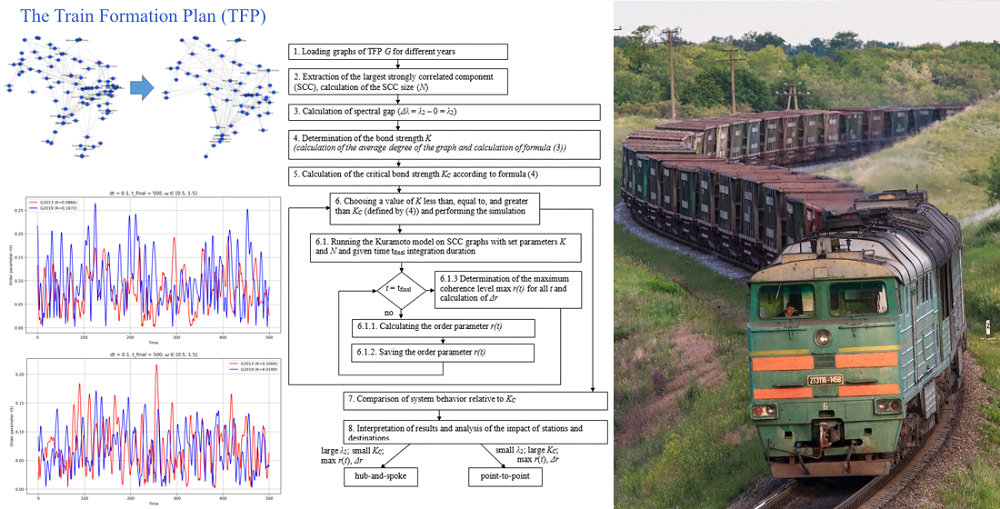
Об’єктом дослідження є процес перевезень вантажів у залізничній мережі, що формалізований у вигляді плану формування поїздів (ПФП) як складної динамічної системи. Для оцінки динамічних властивостей моделі перевезень вантажів на макрорівні функціонування залізничної системи розроблено метод аналізу швидкості передачі вагонопотоків в мережі. Запропонований метод відображає динаміку узгодження не через час фізичного проходження поїздів в мережі, а через здатність системи організації вагонопотоків в поїзди швидко формувати когерентний стан. Для визначення швидкості узгодження застосовано модель Курамото. Це дозволило розрізняти мережі ПФП.

Застосування розробленого методу та проведення моделювання дозволило порівняти структурно-динамічні властивості діючої системи перевезень в період між 2013–2019 рр. Доведена обмежена здатність мереж ПФП до глобальної фазової інтеграції. Встановлено, що мережа ПФП у 2019 році демонструє втрату системної узгодженості, що властиво децентралізованим мережам перевезень типу point-to-point. Це підтверджують розрахунки  та , де різниця між спектральними розривами сягає два порядки, а час досягнення максимуму параметру порядку rmax у 2019 році у 4,07 рази більший при порівнянних значеннях порядку та KC = 6. Це свідчить про трансформацію операційної моделі від централізованої hub-and-spoke у 2013 році до більш децентралізованої point-to-point у 2019 році.

Особливість отриманих результатів в рамках дослідження полягає у тому, що запропонований метод дозволяє підвищити якість макроаналізу зміни структурно-динамічної ефективності мережі ПФП.

Сферою практичного застосування результатів є залізнична галузь. Умовами практичного застосування результатів дослідження є важливість врахування отриманих результатів при аналізі діючих ПФП

Біографії авторів

Андрій Миколайович Киман, Український державний університет залізничного транспорту

Кандидат технічних наук, доцент

Кафедра управління вантажною і комерційною роботою

Андрій Володимирович Прохорченко, Український державний університет залізничного транспорту

Доктор технічних наук, професор

Кафедра управління експлуатаційною роботою

Артем Сергійович Панченко, Харківський національний університету ім. В. Н. Каразіна

Доктор філософії, доцент

Кафедра теоретичної та прикладної інформатики

Сергій Анатолійович Золотрьов, Український державний університет залізничного транспорту

Аспірант

Кафедра управління експлуатаційною роботою

Михайло Анатолійович Кравченко, ТОВ «Кернел-Трейд»

Доктор філософії

Департамент перевалки та флоту  дивізіону логістики

Галина Олегівна Прохорченко, Український державний університет залізничного транспорту

Кандидат технічних наук, доцент

Кафедра управління експлуатаційною роботою

Олександра Олександрівна Орда, Харківський національний автомобільно-дорожній університет

Кандидат технічних наук, доцент

Кафедра транспортних технологій

Посилання

  1. Strong, J. S. (2024). Operating innovation in North American railroads: Activist investors and precision scheduling railroading. Case Studies on Transport Policy, 15, 101164. https://doi.org/10.1016/j.cstp.2024.101164
  2. Butko, T., Prokhorchenko, A., Golovko, T., Prokhorchenko, G. (2018). Development of the method for modeling the propagation of delays in non­cyclic train scheduling on the railroads with mixed traffic. Eastern-European Journal of Enterprise Technologies, 1 (3 (91)), 30–39. https://doi.org/10.15587/1729-4061.2018.123141
  3. Li, B., Jiang, S., Zhou, Y., Xuan, H. (2023). Optimization of train formation plan based on technical station under railcar demand fluctuation. Journal of Industrial and Production Engineering, 40 (6), 448–463. https://doi.org/10.1080/21681015.2023.2221699
  4. Frisch, S., Hungerländer, P., Jellen, A., Lackenbucher, M., Primas, B., Steininger, S. (2022). Integrated freight car routing and train scheduling. Central European Journal of Operations Research, 31 (2), 417–443. https://doi.org/10.1007/s10100-022-00815-3
  5. Butko, T., Prokhorov, V., Chekhunov, D. (2017). Devising a method for the automated calculation of train formation plan by employing genetic algorithms. Eastern-European Journal of Enterprise Technologies, 1 (3 (85)), 55–61. https://doi.org/10.15587/1729-4061.2017.93276
  6. JSC “Ukrainian railways”. Available at: https://www.uz.gov.ua/cargo_transportation Last accessed: 12.08.2025
  7. But’ko, T., Prokhorchenko, A. (2013). Investigation into Train Flow System on Ukraine’s Railways with Methods of Complex Network Analysis. American Journal of Industrial Engineering, 1 (3), 41–45.
  8. Zhang, X., Zhu, T. (2023). Emergence of synchronization in Kuramoto model with general digraph. Discrete and Continuous Dynamical Systems – B, 28 (3), 2335–2390. https://doi.org/10.3934/dcdsb.2022172
  9. Daganzo, C. F., Geroliminis, N. (2008). An analytical approximation for the macroscopic fundamental diagram of urban traffic. Transportation Research Part B: Methodological, 42 (9), 771–781. https://doi.org/10.1016/j.trb.2008.06.008
  10. Wang, Y., Yu, X., Guo, J., Papamichail, I., Papageorgiou, M., Zhang, L. et al. (2022). Macroscopic traffic flow modelling of large-scale freeway networks with field data verification: State-of-the-art review, benchmarking framework, and case studies using METANET. Transportation Research Part C: Emerging Technologies, 145, 103904. https://doi.org/10.1016/j.trc.2022.103904
  11. de Jong, G., Vierth, I., Tavasszy, L., Ben-Akiva, M. (2012). Recent developments in national and international freight transport models within Europe. Transportation, 40 (2), 347–371. https://doi.org/10.1007/s11116-012-9422-9
  12. Butko, T., Muzykin, M., Prokhorchenko, A., Nesterenko, H., Prokhorchenko, H. (2019). Determining the Rational Motion Intensity of Train Traffic Flows on the Railway Corridors with Account for Balance of Expenses on Traction Resources and Cargo Owners. Transport and Telecommunication Journal, 20 (3), 215–228. https://doi.org/10.2478/ttj-2019-0018
  13. Szymula, C., Bešinović, N., Nachtigall, K. (2024). Quantifying periodic railway network capacity using petri nets and macroscopic fundamental diagram. Transportation Research Part C: Emerging Technologies, 158, 104436. https://doi.org/10.1016/j.trc.2023.104436
  14. Khomenko, Y., Okorokov, A., Matsiuk, V., Zhuravel, I., Pavlenko, O. (2025). Revealing the causes of delays at transit points along an intermodal grain supply chain. Eastern-European Journal of Enterprise Technologies, 4 (3 (136)), 40–50. https://doi.org/10.15587/1729-4061.2025.338166
  15. Helbing, D. (2001). Traffic and related self-driven many-particle systems. Reviews of Modern Physics, 73 (4), 1067–1141. https://doi.org/10.1103/revmodphys.73.1067
  16. Saw, V.-L., Chung, N. N., Quek, W. L., Pang, Y. E. I., Chew, L. Y. (2019). Bus bunching as a synchronisation phenomenon. Scientific Reports, 9 (1). https://doi.org/10.1038/s41598-019-43310-7
  17. Kuramoto, Y.; Araki, H. (Ed.) (1975). Lecture Notes in Physics, International Symposium on Mathematical Problems in Theoretical Physics. Vol. 39. New York: Springer-Verlag, 420.
  18. Rodriguez, M., Fathy, H. K. (2022). Distributed Kuramoto Self-Synchronization of Vehicle Speed Trajectories in Traffic Networks. IEEE Transactions on Intelligent Transportation Systems, 23 (7), 6786–6796. https://doi.org/10.1109/tits.2021.3062178
  19. Fretter, C., Krumov, L., Weihe, K., Müller-Hannemann, M., Hütt, M.-T. (2010). Phase synchronization in railway timetables. The European Physical Journal B, 77 (2), 281–289. https://doi.org/10.1140/epjb/e2010-00234-y
  20. Yoon, S., Sorbaro Sindaci, M., Goltsev, A. V., Mendes, J. F. F. (2015). Critical behavior of the relaxation rate, the susceptibility, and a pair correlation function in the Kuramoto model on scale-free networks. Physical Review E, 91 (3). https://doi.org/10.1103/physreve.91.032814
  21. Wang, Y., Doyle, F. J. (2013). Exponential Synchronization Rate of Kuramoto Oscillators in the Presence of a Pacemaker. IEEE Transactions on Automatic Control, 58 (4), 989–994. https://doi.org/10.1109/tac.2012.2215772
  22. Wang, W., Du, W., Liu, K., Tong, L. (2022). The Evolution of China’s Railway Network (CRN) 1999-2019: Urbanization Impact and Regional Connectivity. Urban Rail Transit, 8 (2), 134–145. https://doi.org/10.1007/s40864-022-00168-9
  23. Peng, S., Lu, J., Jiang, B., Zhu, J. (2024). Synchronization of high-dimensional Kuramoto-oscillator networks with variable-gain impulsive coupling on the unit sphere. Nonlinear Analysis: Hybrid Systems, 54, 101536. https://doi.org/10.1016/j.nahs.2024.101536
  24. Lei, L., Han, W., Yang, J. (2021). Kuramoto model with correlation between coupling strength and natural frequency. Chaos, Solitons & Fractals, 144, 110734. https://doi.org/10.1016/j.chaos.2021.110734
  25. Böhle, T., Kuehn, C., Thalhammer, M. (2021). On the reliable and efficient numerical integration of the Kuramoto model and related dynamical systems on graphs. International Journal of Computer Mathematics, 99 (1), 31–57. https://doi.org/10.1080/00207160.2021.1952997
  26. Gherardini, S., Gupta, S., Ruffo, S. (2018). Spontaneous synchronisation and nonequilibrium statistical mechanics of coupled phase oscillators. Contemporary Physics, 59 (3), 229–250. https://doi.org/10.1080/00107514.2018.1464100
  27. McGraw, P. N., Menzinger, M. (2007). Analysis of nonlinear synchronization dynamics of oscillator networks by Laplacian spectral methods. Physical Review E, 75 (2). https://doi.org/10.1103/physreve.75.027104
  28. O’Kelly, M. E., Park, Y. (2023). Contrasts in Sustainability between Hub-Based and Point-to-Point Airline Networks. Sustainability, 15 (20), 15111. https://doi.org/10.3390/su152015111
  29. Sabhahit, N. G., Khurd, A. S., Jalan, S. (2024). Prolonged hysteresis in the Kuramoto model with inertia and higher-order interactions. Physical Review E, 109 (2). https://doi.org/10.1103/physreve.109.024212
  30. Arenas, A., Díaz-Guilera, A., Kurths, J., Moreno, Y., Zhou, C. (2008). Synchronization in complex networks. Physics Reports, 469 (3), 93–153. https://doi.org/10.1016/j.physrep.2008.09.002
Розрока методу аналізу швидкості передачі вагонопотоків у плані формування поїздів на основі теорії синхронизації в складних мережах

##submission.downloads##

Опубліковано

2025-10-31

Як цитувати

Киман, А. М., Прохорченко, А. В., Панченко, А. С., Золотрьов, С. А., Кравченко, М. А., Прохорченко, Г. О., & Орда, О. О. (2025). Розрока методу аналізу швидкості передачі вагонопотоків у плані формування поїздів на основі теорії синхронизації в складних мережах. Eastern-European Journal of Enterprise Technologies, 5(3 (137), 56–67. https://doi.org/10.15587/1729-4061.2025.341559

Номер

Том 5 № 3 (137) (2025): Процеси управління

Розділ

Процеси управління

Ліцензія

Авторське право (c) 2025 Andrii Kyman, Andrii Prokhorchenko, Artem Panchenko, Serhii Zolotarov, Mykhailo Kravchenko, Halyna Prokhorchenko, Oleksandra Orda

Creative Commons License

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.

Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.

Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.